直径15cmの円の円周の長さを求めよ。 直径 7 2 cmの円の円周の長さを求めよ。 半径x cmの円の周の長さを求めよ。 直径t cmの円の周の長さを求めよ。 次の問いに答えよ。 半径4cmの円の面積を求めよ。 半径12cmの円の面積を求めよ。 直径16cmの円の面積を求めよ 今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周問題 円の面積の解き方を覚えて計算力をつける為に、次の円の問題を計算しましょう。 問1. π(パイ)とは何のことですか? 問2. π(パイ)はいくつですか?小数第二位まで答えなさい。 問3. 半径をrとしたとき、円の面積を求める式を答えましょう。

面積問題 小学4から6年生 算数問題プリント
円の面積 問題 難しい
円の面積 問題 難しい-円の面積の解説 円の面積は 半径×半径×円周率=面積 で求めることができます。半径をr、円周率をπ、面積をSとすると S=πr 2 となります。 円の面積を 解説 まず、正方形は円に内接しているので、 対角線の長さは、円の直径の長さと等しく cm ですよね もしくは、内側の正方形をくるっと回転させて こうなるから、底辺 cm , 高さ 10cm の三角形2つ分の面積で 2 × 1 2 × × 10 = 2 × 1 2 × × 10 = 言われてみれば意外と簡単でしたね! はかせちゃん はかせは昔、和同開珎を拾ったことがあるのです、
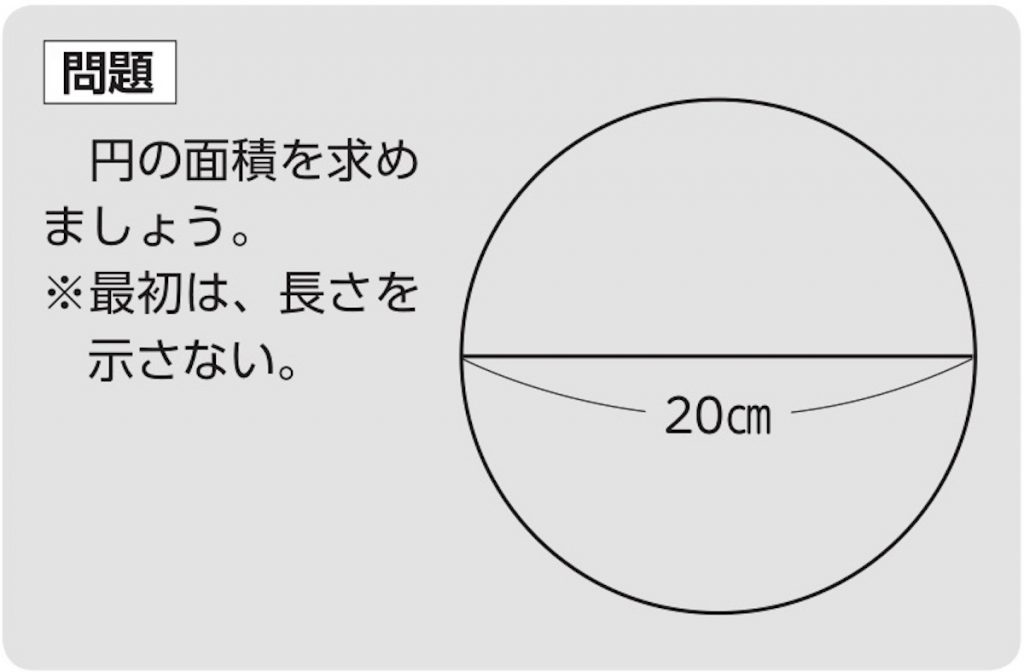



小6算数 円の面積 指導アイデア みんなの教育技術
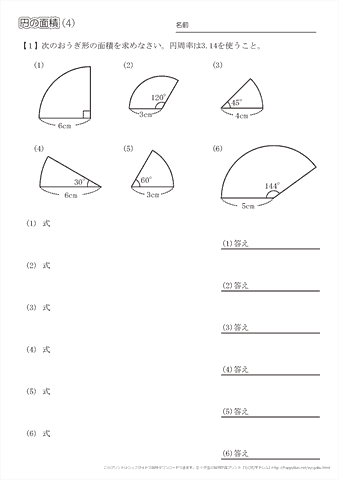
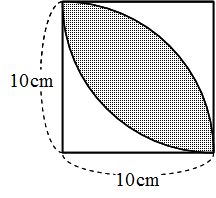
台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 例題 半径5cmの半円を、円Aを中心にして、45°回転させました。 黒くぬった部分の面積を求めなさい。おうぎ形の面積 を 求める力 が、理解できていれば、小学生が自分の力で、解答を導けるプリントを作りました♪パパママ向けのヒント解説も行っていますよ♪ 正方形の面積は80㎠なので、正方形の1辺を ㎝とすると、 × =80 よって、直径×直径=80 すると半径×半径も分かります。 <答え> 直径×直径=80なので、半径×半径=(直径÷2)×(直径÷2)=直径÷4=となります。 よってこの円の面積は×314=628(㎠)
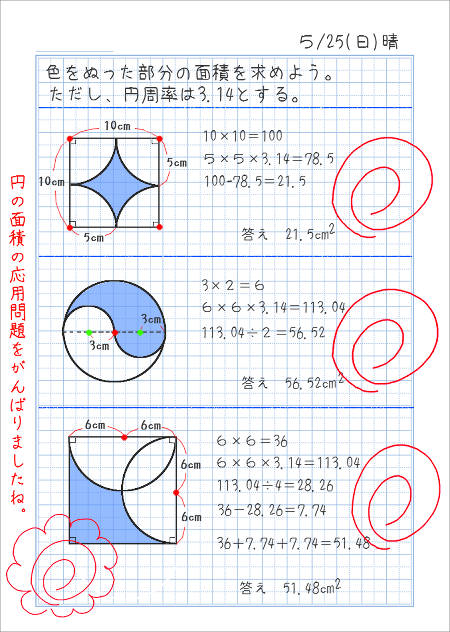
小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分円の面積 小学6年生 計算無料プリント 小学生算数問題円の面積を求める為の名称や公式をまず理解します。円周率は、314で計算していますどんな面積も考え方は同じで、応用問題の場合は隠された半径を見つけだすのがポイントです。半径を探す謎解き問 問題 (正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する) 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の
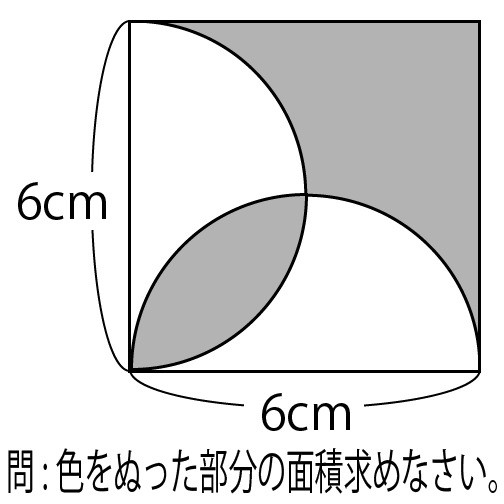
円の面積(4) 円の面積(5) 2 文字と式 文字を使った式に表そう(1) 問題一括 (3,127Kb) 解答一括 (3,5Kb) 文字を使った式に表そう(2) 文字を使った式に表そう(3) 3 分数のかけ算 分数×分数(1) 問題一括 (3,354Kb) 解答一括 (3,775Kb) 分数×分数(2) 力をつけよう(1) 力を 大きい円の半径は8cm(4+4)なので面積は、 8×8×314=096㎠ 半円の半径は4cmなので面積は、 4×4×314×1/2=2512㎠ この半円が4つあるので、 2512×4=㎠ 大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え(1)円について,次の部分は何と言いますか。その用語を の中にかきなさい。 ア キ イ カ オ ウ エ (2)半径が3㎝の円の直径と円周の長さ,面積を求めなさい。 (3)円の面積が5024㎝2になりまし
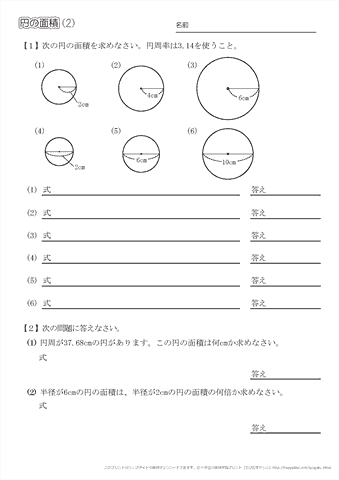



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




半円を回転させる面積の問題 プリントを使って自分で解こう
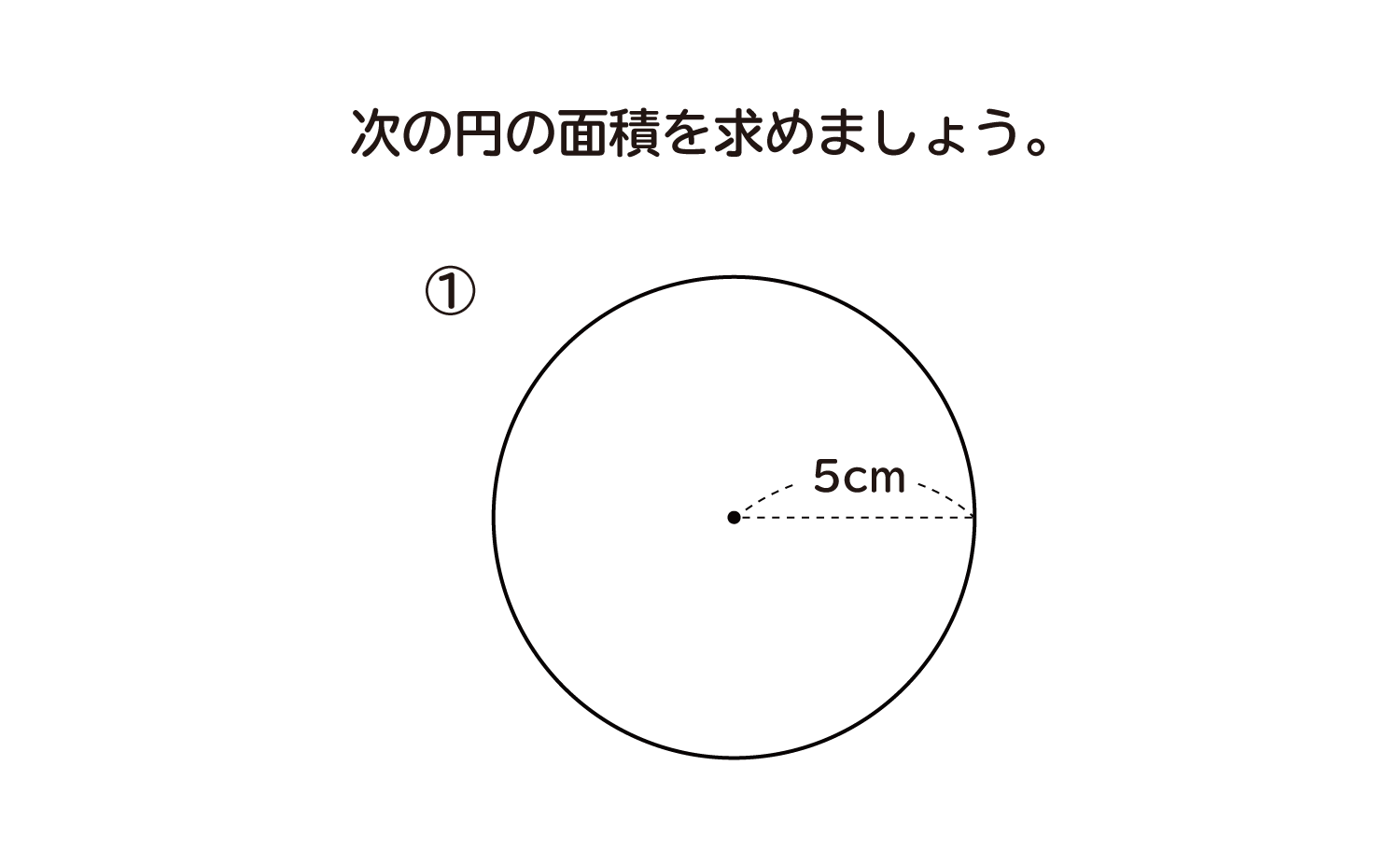
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引くこのページは、小学6年生で習う「円の面積を求める問題集」が無料でダウンロードできるページです。 この問題のポイント ・ 円の面積は「半径×半径×円周率(314)」 という公式を使って求めます。 四分円の面積の計算問題 続いて、四分の一の円の大きさを求めましょう。 例題 半径3cmの四分円の面積を求めてみましょう。 解答 こちらも上の計算式を元に算出します。 314×3×3÷4=7065cm2と計算できるのです。 まとめ




おうぎ形 の弧の長さと面積 計算ドリル 問題集 数学fun
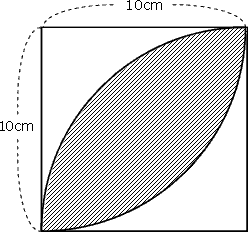



面積の求め方 算数の教え上手 学びの場 Com
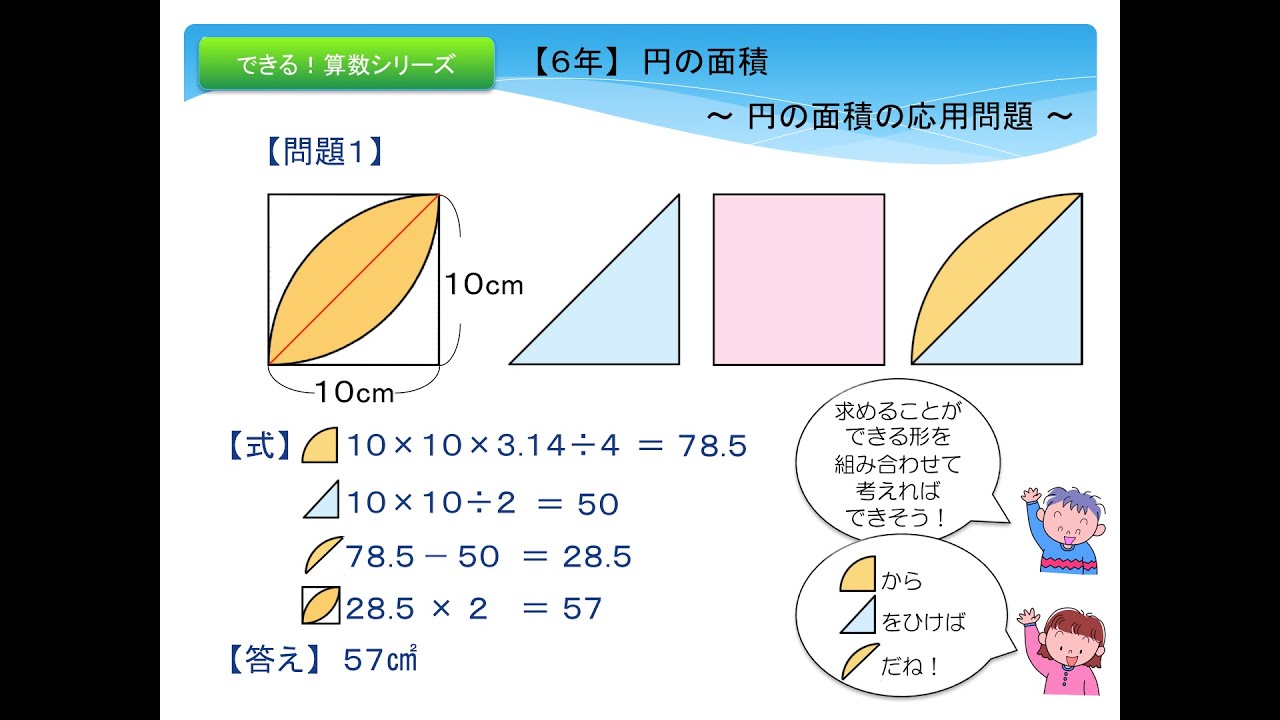
小学6年 「円の面積」 1/5時の学習プラン ~ 半径10㎝の円の面積について、見当を付けてみよう ~ 1 本時の目標 円の面積の大きさについて見当を付けようとする。 算数への関心・意欲・態度 2 算数的活動について (ア) 探究的な活動として、円 正方形の面積=,10×10=100 (㎠) 100:面積=1:057 面積=57㎠ と求めることができる。 円周率が314の時しか使えません。等積変形という問題を解説していきます。 等積変形というのは 面積の等しい三角形を見つける問題や 面積が等しくなるように図形を変形する問題です。 まずは、等積変形をやっていく上で とっても大切な基礎の部分を学習しておきましょう。
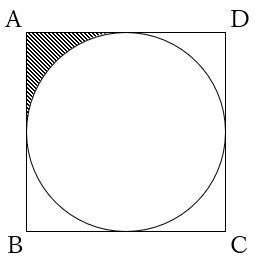



半径の分からない円の面積 中学受験プロ講師ブログ
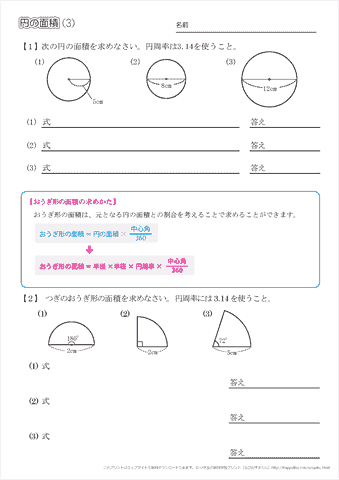



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
第6問 長方形と内接円 5年生 内接円 円 長方形 面積の和 ★★☆☆☆☆(小学4〜5年生対象)半径22cmの円の周の長さを求めよ。 半径12cmの円の面積を求めよ。 直径19cmの円の周の長さを求めよ。 直径15cmの円の面積を求めよ。 次の問いに答えよ。 円周の長さが14πcmの円の面積を求めよ。 円周の長さが8xπcmの円の面積を求めよ。第173問 複合図形の面積 図形ドリル 5年生 6年生 円 長方形 面積 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げてい



6年算数 円の面積 2 わかる教え方




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
適度な難易度の面積の問題を90問集めました。 1ページ3問ずつで,式や筆算を書き込むスペースが十分あるので大変学習しやすくなっています。 また,解答解説はこれ以上ありえない位くわしく書いてあります。 面積の問題のPDFはこちら↓↓ 面積の問題 面積の問題解答・解説 面積の問題解答のみ長方形の縦の長さは,円の半径,横の長さは,円周の半分と同じになります。 積の公式は次のようになります。 円の面積=半径×円周の半分 円周 半分 直径 =半径×半径×314 円の面積 チャレンジシート① 学ぶ 円の面積=半径×半径×314 円周の半分(半径×314) 半径 横 縦面積の基本問題(中学受験 算数問題) 正方形内の円(本郷中学 算数第①回入試問題 10年) 正方形の回転(中学受験算数 図形の回転)
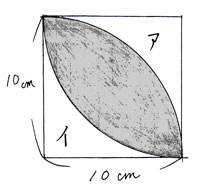



円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム




面積問題 小学4から6年生 算数問題プリント
サンパズ! 6年生プリント目次 分数のかけ算とわり算と逆数 対称な図形と円の面積 文字を使った式と比 速さ・道のり・時間 応用プリント チャレンジプリントダウンロード小学校6年生で習う「円」の面積 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに円の面積の解説についてはこちらに詳しく説明しています。平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める おうぎ形2_半径と弧から,面積を




はっぱ型 の図形の面積 身勝手な主張




円の面積の応用 小学校6年算数より 身勝手な主張
円周角の定理を使わずに解け! 中学受験 算数 数学難問 小学生 中学生 805 You're signed out Videos you watch may be added to the TV's watch history and円の面積は、半径を1辺とする正方形の面積の2倍と4倍の間にあることを調べる。 作業的な活動 円の面積の見当を付けて、 1c㎡ の正方形がいくつ分あるか、方眼を用いて調べる。 円を等分して、平行四辺形などの既習の求積可能な図形に変形する。問題16 図の黒い部分の面積は24c㎡です。外側の正六角形の面積を求めなさい。 → 解答 問題17 たて10cm、よこ15cmの長方形の中に半径2cmの円があります。この円が長方形の内側をまわりにそって回るとき、円の通らない部分の面積を求めなさい。




世界一分かりやすい算数 小6 円の面積




おうぎ形に関する応用問題3選
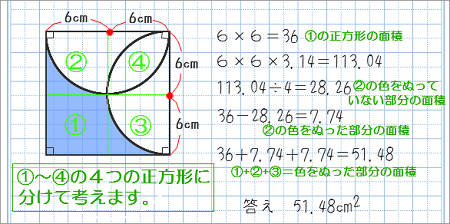
よく出る 円の面積問題 小学6年生 円の面積を求める為の名称や公式をまず理解します。 どんな面積も考え方は同じで、応用問題の場合は隠された半径を見つけだすのがポイントです。 四角形や三角形と組み合わせて円の面積が組み合わさっています。 直径や半径を探す謎解き問題と思ってください。 角度の問題は、円の角度/360で計算しましょう! つぎに面積。 おうぎ形って円の一部だから、おうぎ形の面積=円の面積の一部です。 だから(円の面積)× \(\frac{1}{4}\) をすればいい。 円の面積は $$ 6 \times 6 \times \pi = 36 \pi $$ よって、求めるおうぎ形の面積は $$ 36 \pi \times \frac{1}{4} = 9 \pi $$ 答.\(9 \pi \) ㎠ と出ます。



円の面積問題のようですが 筑波大学附属中学 2008年 パズル算数クイズ
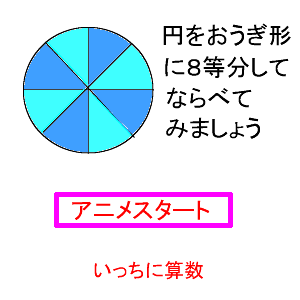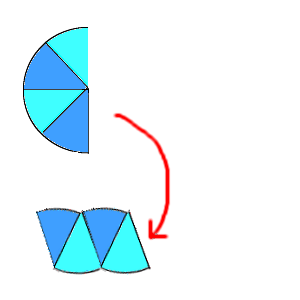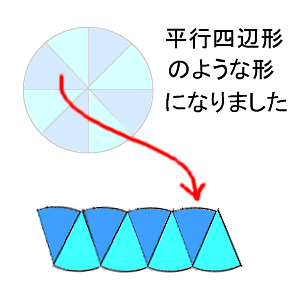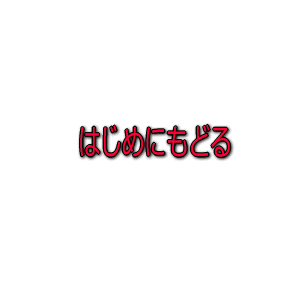



6年算数 円の面積 2 わかる教え方



円 これが中学入試に出た図形問題




小6算数 円の面積 指導アイデア みんなの教育技術




意外に知らない 知っていると得する 円の面積問題 恋する中高一貫校 適性検査 徹底攻略



小学6年生 算数 無料問題集 円の面積 おかわりドリル
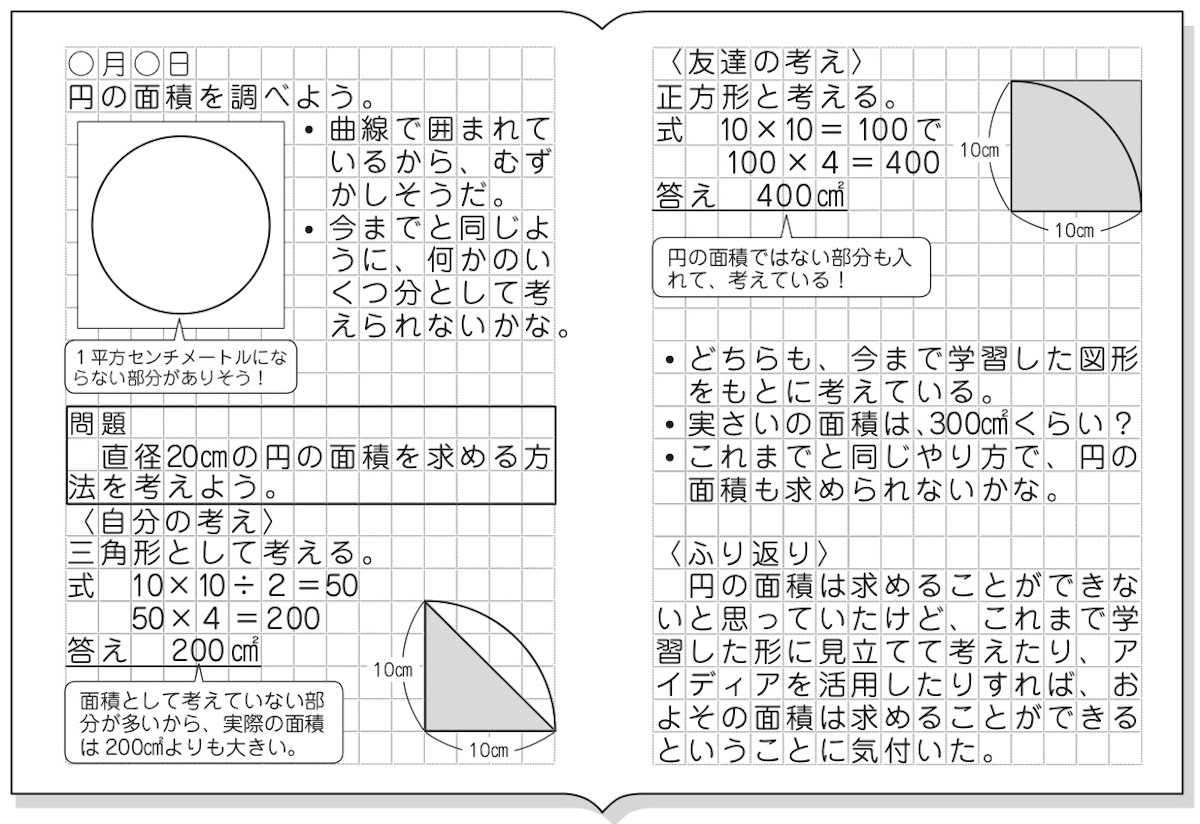



小6算数 円の面積 指導アイデア みんなの教育技術




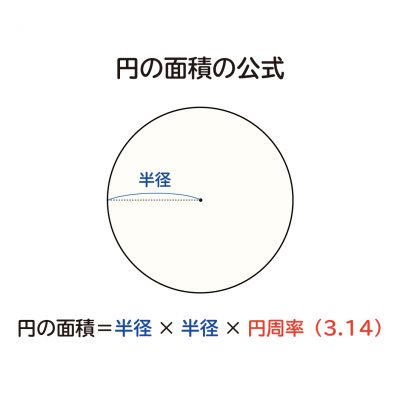
円の面積の公式 算数の公式



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




浅野 円の面積を比べる ジーニアス 中学受験専門塾
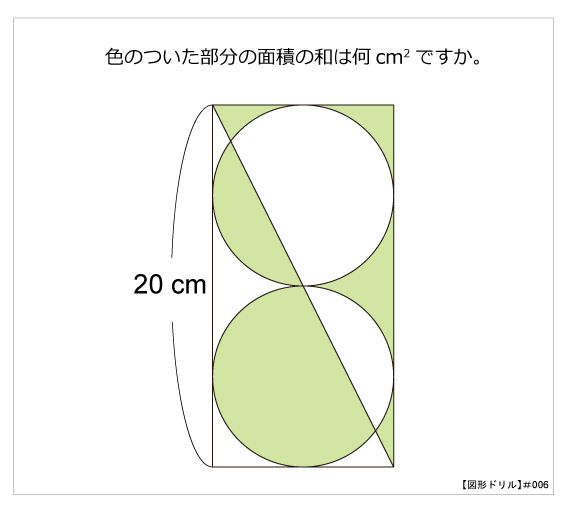



図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦 図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦




6年生算数ドリル 円
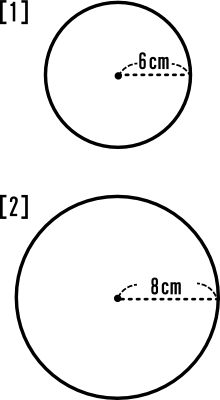



中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形




円の面積 その2 家庭学習レシピ




いろいろな円の面積 無料で使える学習ドリル



円の面積問題 開成中学 2011年 これが中学入試に出た図形問題




15年度 愛光中学校 算数 1 6 面積



算数 三日月形 半円 の面積の応用問題 なるほどの素



円 これが中学入試に出た図形問題
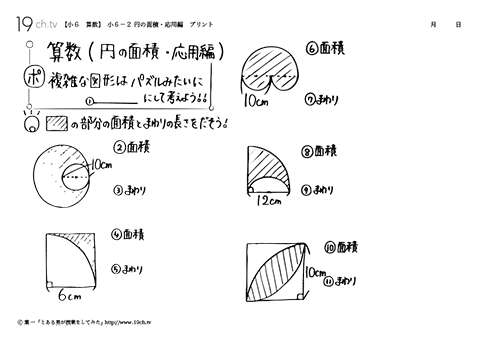



小学6年生の算数 動画 円の面積 応用編の問題 19ch



3




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



面積を求める応用問題2 数学総復習




円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチニュース
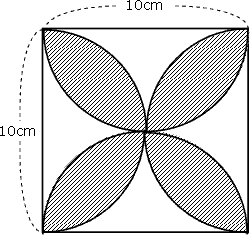



面積の求め方 算数の教え上手 学びの場 Com
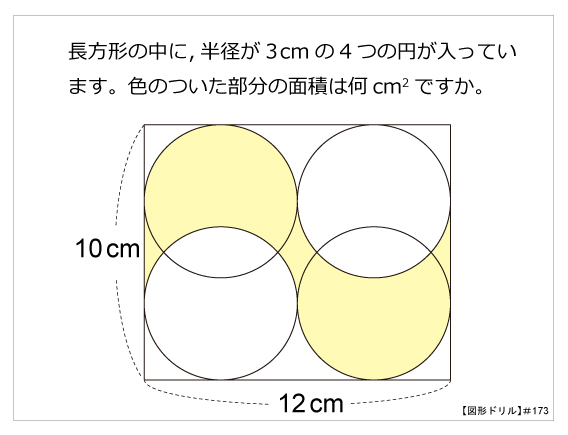



図形ドリル 第173問 複合図形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦




円の面積 その1 家庭学習レシピ



面積 これが中学入試に出た図形問題




Descubre Como Resolverlo En Qanda
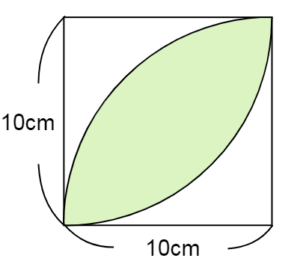



小学6年生 円の面積 問題プリント まとめテスト 無料の塾プリント
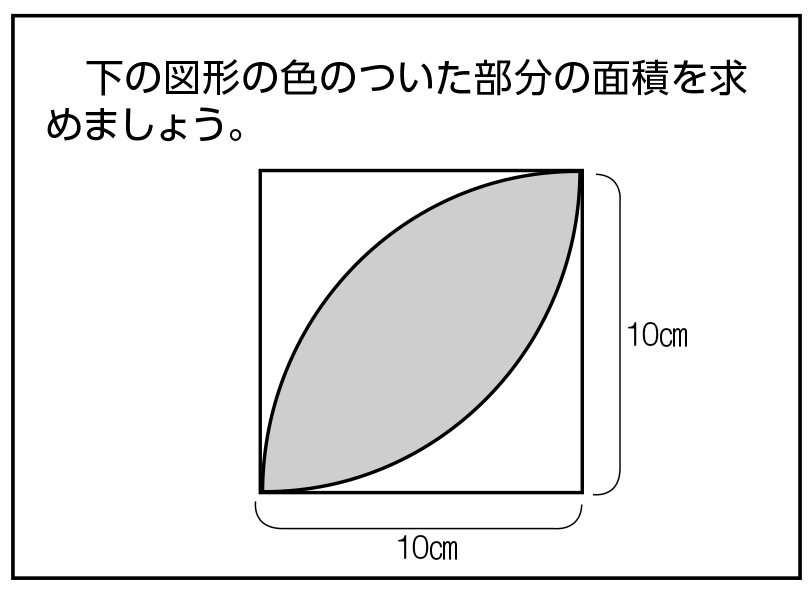



小6算数 円の面積 指導アイデア 2 みんなの教育技術




小6 算数 小6 旧 円の面積 Youtube




世界一分かりやすい算数 小6 円の面積
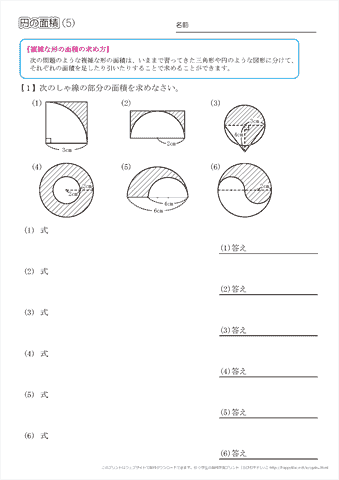



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素



長方形と重なった円の部分面積は 女子学院中学 2007年 これが中学入試に出た図形問題



小学6年生の面積の問題です 求め方がわからないので 教えてください よ Yahoo 知恵袋




円の面積 算数用語集
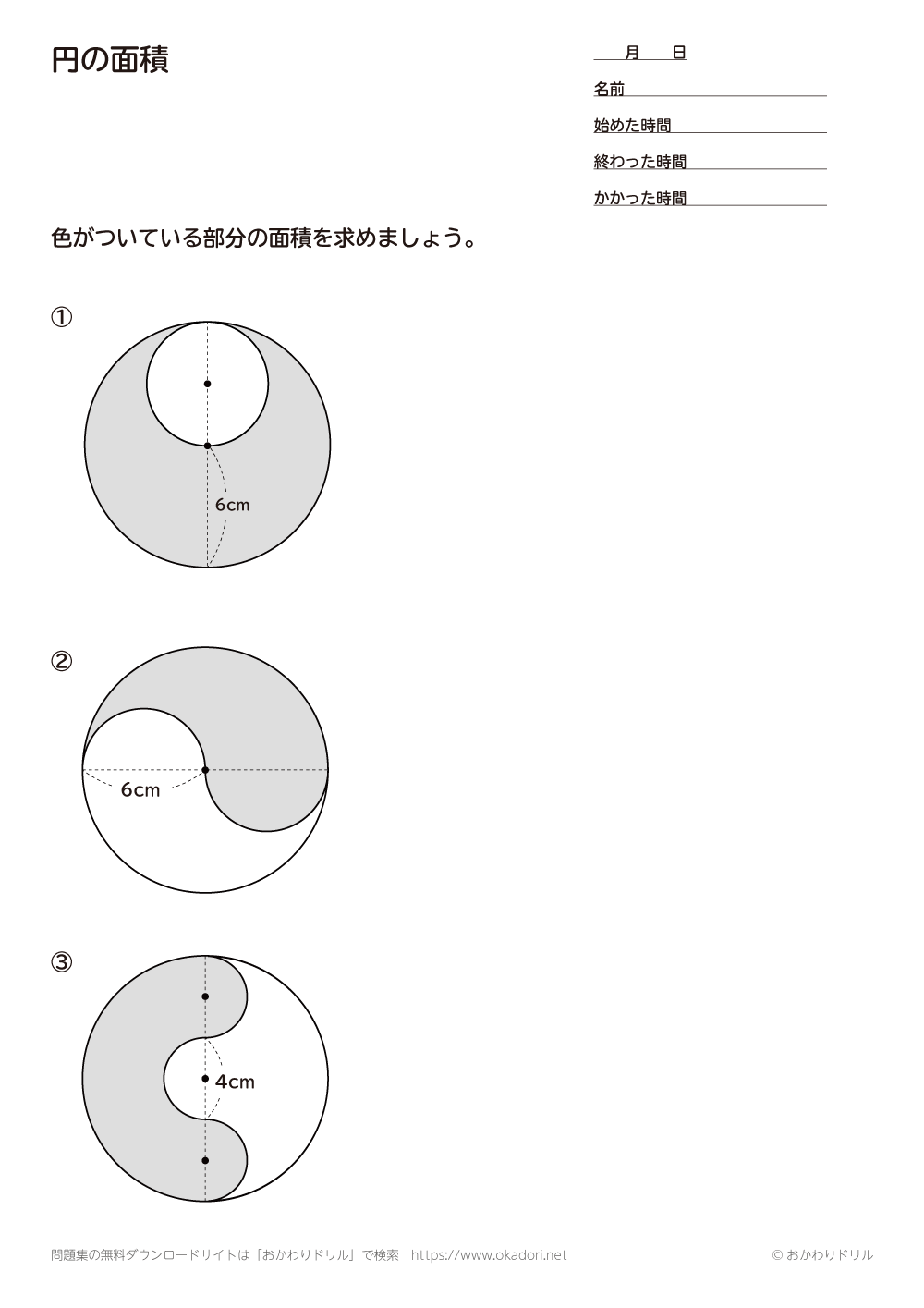



小学6年生 算数 無料問題集 円の面積 おかわりドリル




応用 おうぎ形と正方形の面積 なかけんの数学ノート




無差別級算数 円の面積 受験算数に挑戦
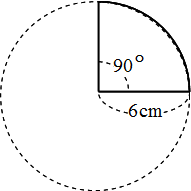



世界一やさしい 円の面積を求める問題の解き方 働きアリ
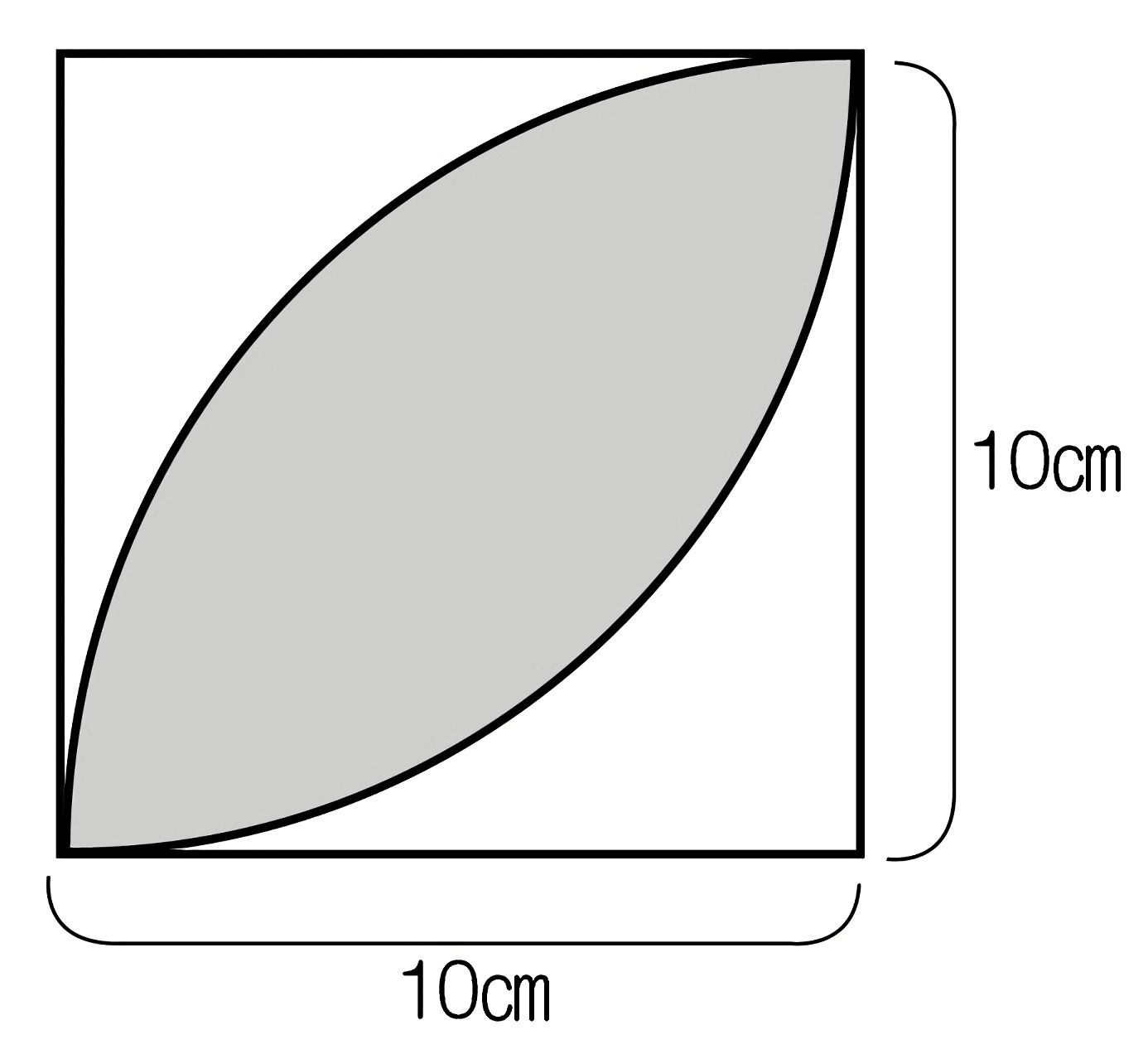



小6算数 円の面積 指導アイデア 2 みんなの教育技術
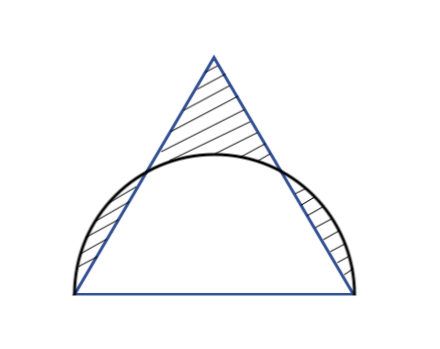



斜線部分の面積を求める問題 よくあるパターン 苦手な数学を簡単に




超頻出 正方形の中に正方形の面積問題 恋する中高一貫校 適性検査 徹底攻略



6年算数 円の面積 2 わかる教え方



入試問題解説 算数 芝浦工業大学柏中 19年度 大問3 中学受験ドットコム
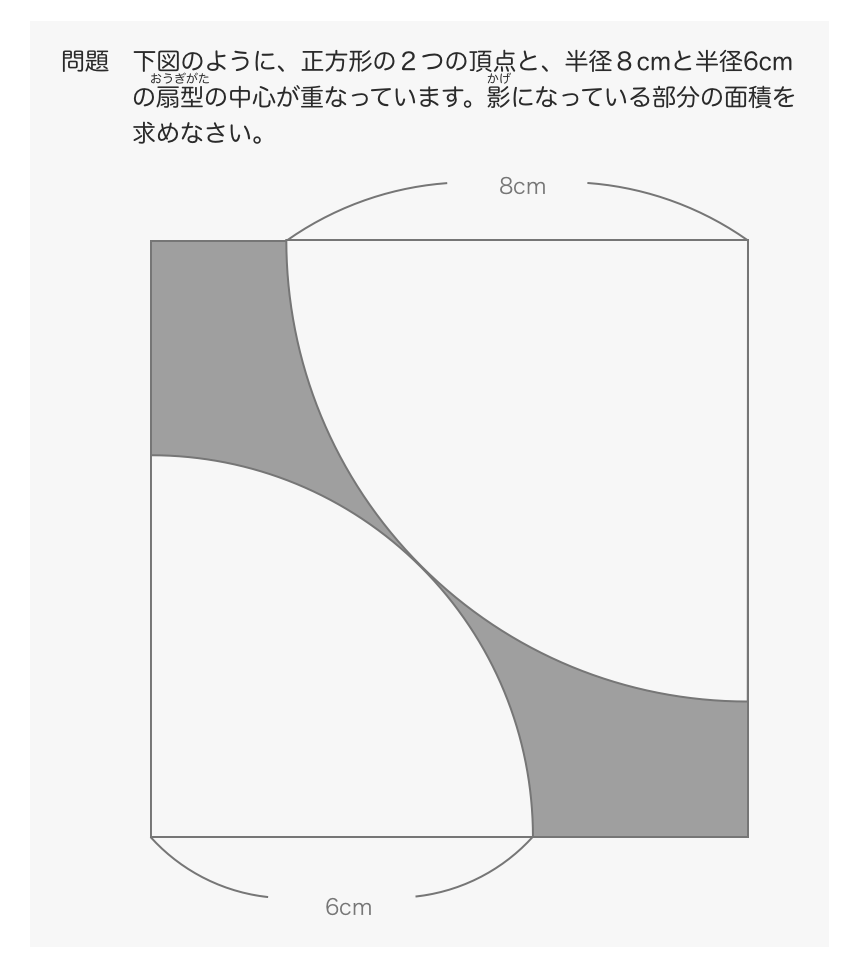



自作教材 円と扇形2 本質と技とコツ カテキョウブログ



ドリルズ 小学6年生 算数 の無料学習プリント算数 円の面積の問題
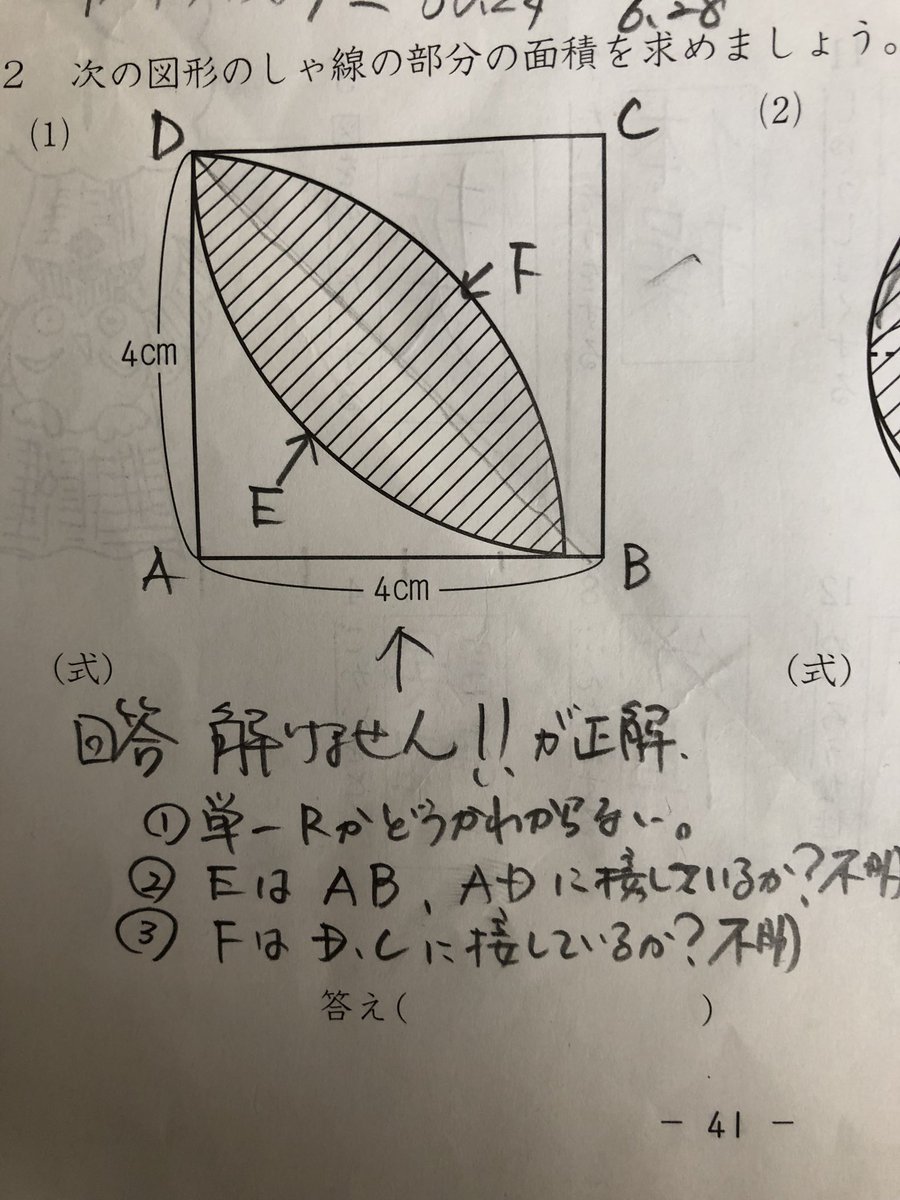



円の面積




円の面積 練習応用 Youtube



円の面積 その2 家庭学習レシピ



スマホok 6年 円の面積 円の面積の応用問題 Youtube



世界一やさしい 円の面積を求める問題の解き方 働きアリ



3




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



今週は灘より1問です 06 05 15 学習塾ロジム 今週の1問




中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋 中学受験 勉強 中学




円の面積の求め方 公式と計算例



1



小6算数 円の面積 指導アイデア 1 みんなの教育技術



小学6年生 算数 無料問題集 円の面積 おかわりドリル



1




山と数学 そして英語 小学校算数 円の面積に関する応用問題



9th Stage 17 重なり合う8つの円の面積問題 数学クイズ なん度 Math Quiz Find Angles



個別進度学習 小6算数 面積問題 に思うこと マナビオ Manabio
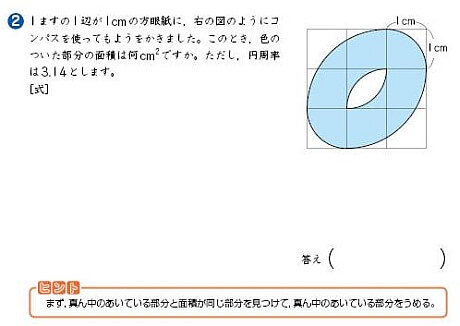



z会の通信教育小学生コース 教材見本 算数




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント




世界一分かりやすい算数 小6 円の面積




円周の求め方の基本問題が解けるようになったら 次は応用問題にも挑戦してみましょう これも 5年生後半から6年生向けの内容です 円周の長さを求める応用 問題を解こう 円周の長さを求める問題で もっと基本 学習ノート 学習 数学ノート



円の面積 その2 家庭学習レシピ
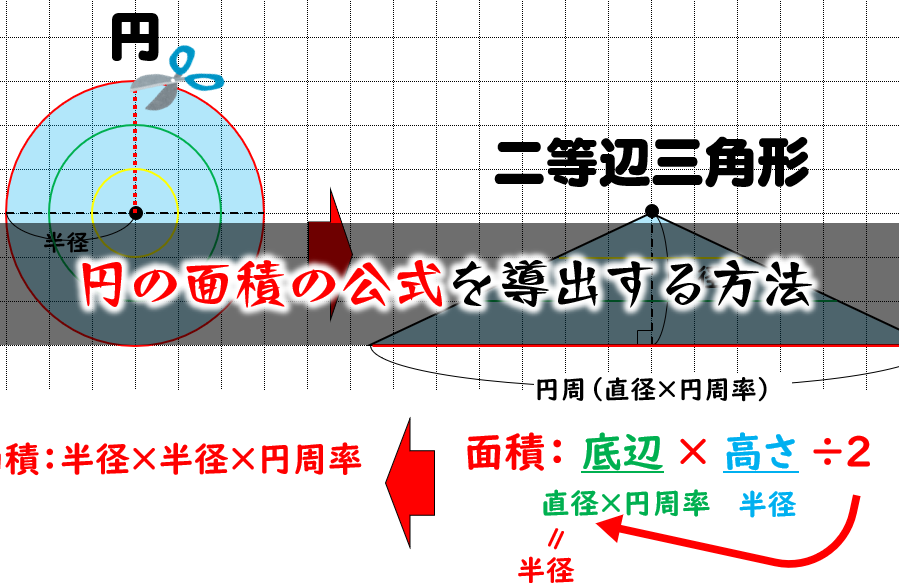



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun



ドリルズ 小学6年生 算数 の無料学習プリント円の面積 円周の問題
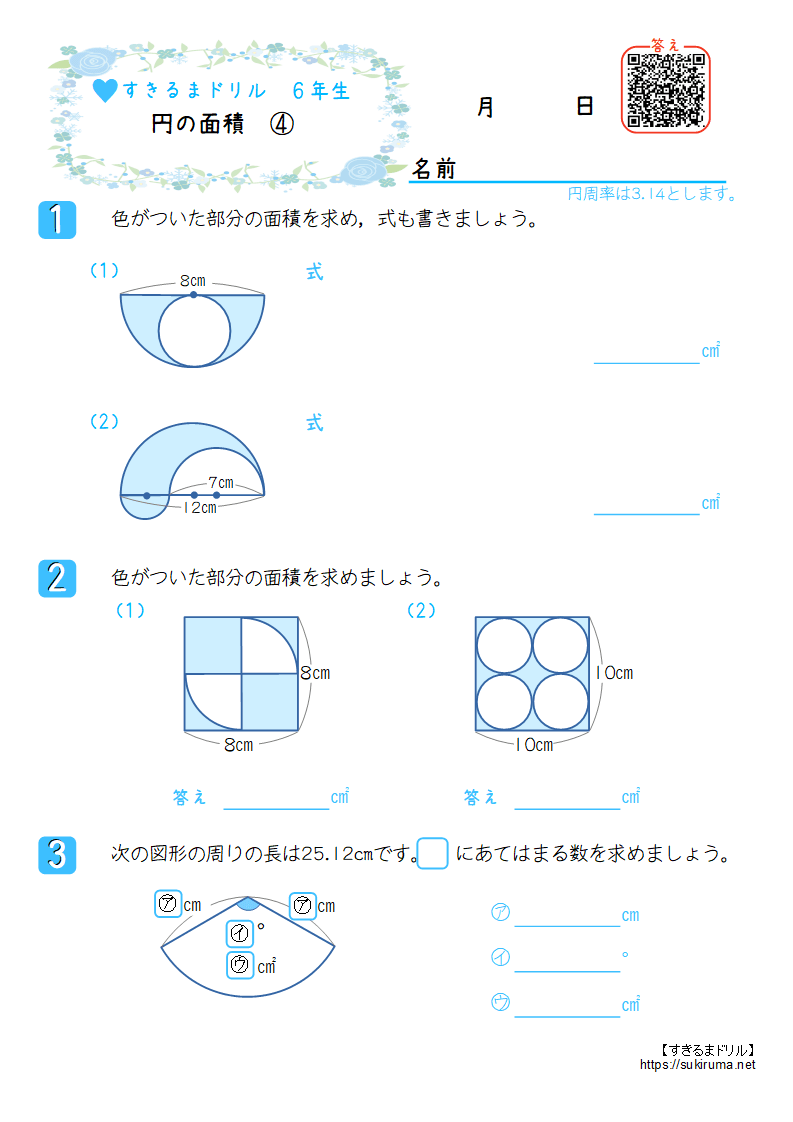



すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 無料学習プリント
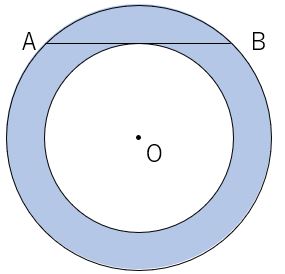



面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




面積の求め方 算数の教え上手 学びの場 Com




面白い算数の問題 円 面積 算数 中学入試 Youtube




円とおうぎ形 応用 無料で使える中学学習プリント



六年生の算数の問題です 円の面積です 写真の を教えてください 式などもよ Yahoo 知恵袋
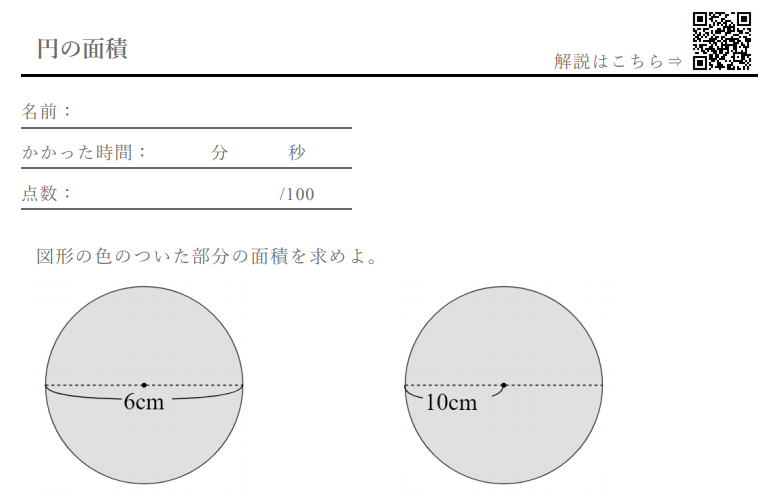



円 の面積 計算ドリル 問題集 数学fun




超頻出 正三角形の中にある正三角形の面積 問題 恋する中学受験 大学受験を見据えた中学受験




小6算数 円の面積 指導アイデア 2 みんなの教育技術
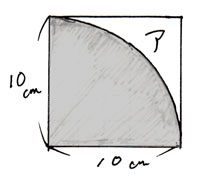



円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム




意外に知らない 知っていると得する 円の面積問題 恋する中高一貫校 適性検査 徹底攻略




円の面積のおもしろ問題3選 美味しそうな色合い なぜか分かる はかせちゃんの怪しい研究室




小6 算数 小6 2 円の面積 応用編 Youtube




世界一分かりやすい算数 小6 円の面積




6年生算数ドリル 円
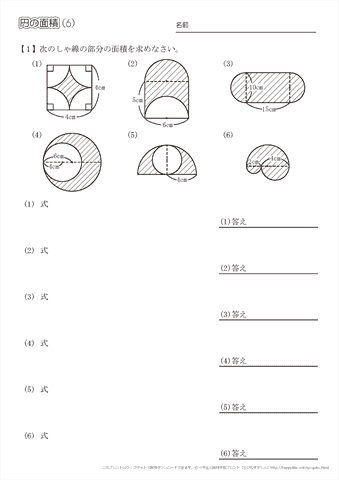



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



Http Www Edu Town Sera Hiroshima Jp Seranishi Es Sidouann Sidouannsyuu Ryoutosokutei 6nennennnomennseki Pdf



0 件のコメント:
コメントを投稿