九点円に関する性質 九点円の半径は外接円の半径の半分 $ abc$ の九点円は,$ m_am_bm_c$ の外接円です.一方,$ m_am_bm_c$ と $ abc$ は相似で,その相似比は $12$ であることから,$ abc$ の九点円の半径が,外接円の半径の半分であることが従います.円の性質を具体的な 場面で活用する。 ③ 与えられた図形の 中に円を見出すこ ができるように する。 ② ワークシートや ノートの記述内 容をもとに確認 する。 めあて 円の性質を証明の根拠として使うことができる。右の図のような円があり,異なる3点 a, b, c は円周上の点である。線分 ac 上に,2点 a, c と異なる点 d をとる。また,2点 b, d を通る直線と円との交点のうち,点 b と異なる点を e とする。 ∠ abe=35°, ∠ cde=80° であるとき, ∠ bec の大きさは何度か。
中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
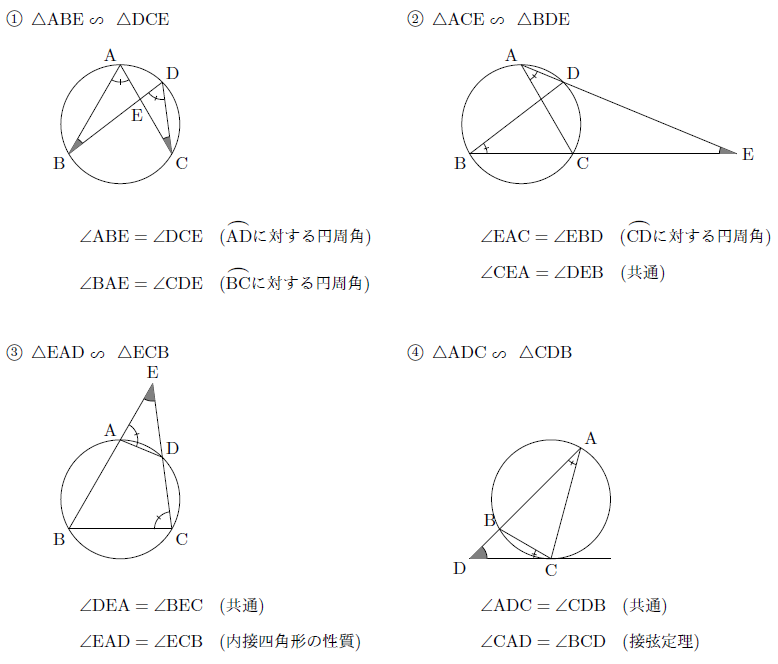
円の性質の証明
円の性質の証明-5図形の性質と証明 円の接線を作図しよう 10 2 年 組 氏名 1 古代ギリシアの数学者ユークリッドは,いくつかの基本的な図形の性質をもとにして, 様々な図形の性質を証明し,有名な「原論」にまとめました。 この原論の第3巻に,「与えられた点から与えられた円に接線をひく」作図の方法が紹介円の性質 2 目標 (1) 円周角と中心角に関心をもち、それらの関係や性質を見い出したり、その証明にどのような図 形の性質が用いられているのかを考えたりしようとしている。 数学への関心・意欲・ 態度 (2)円周角と中心角の関係や 、




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
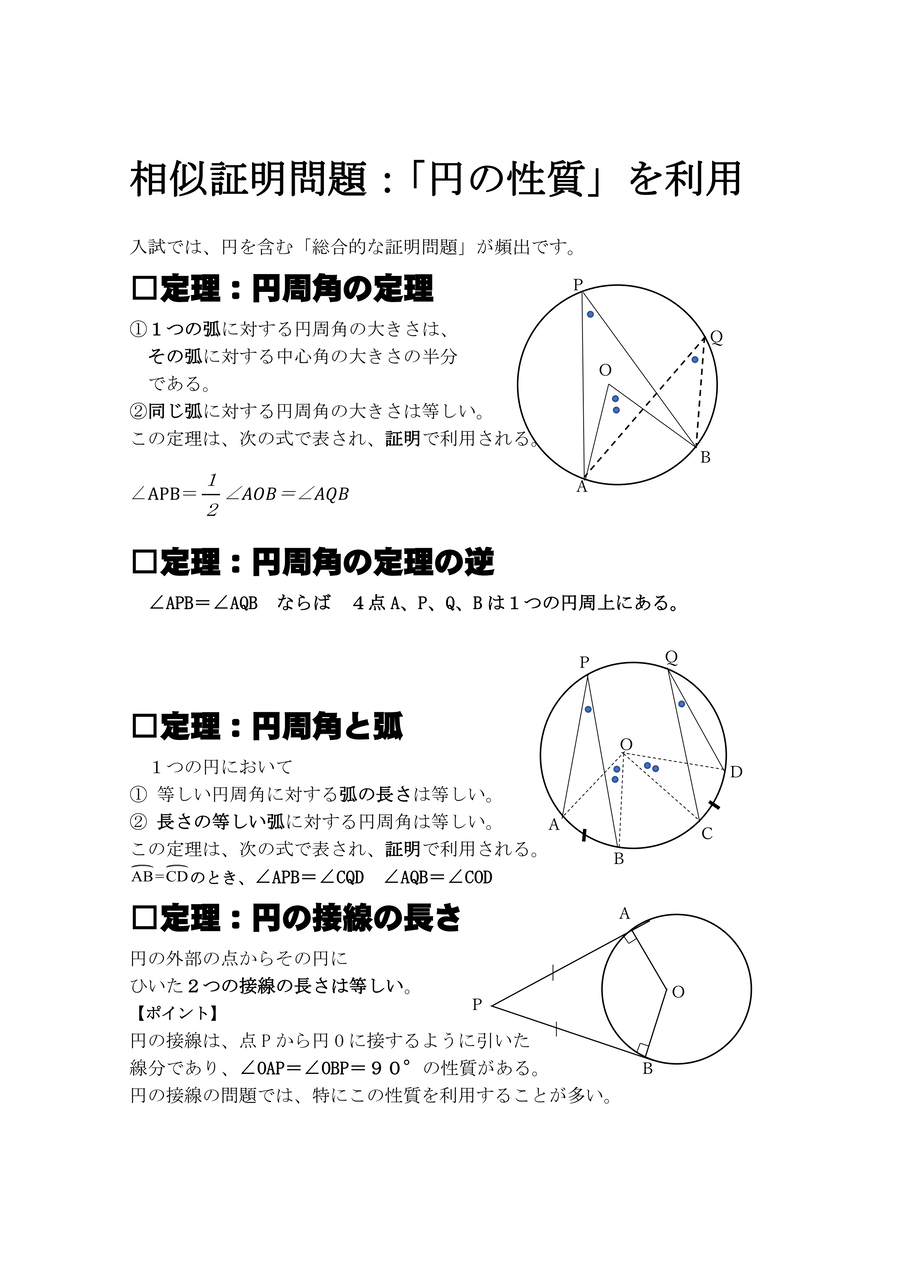
円の外にある 1 点からその円に引いた 2 本の接線の長さは等しい 。 これは以下のように証明ができます。 下の図のように,円 に円の外側の点 から 2 本の接線を引き,その接点を , とする。 と において, 線分 , は円 の接線なので, ① は共通 ②円分多項式 定義1 n 乗して始めて1 になる数を1 の原始n 乗根(primitive nth root) と呼ぶ. n が素数の場合は1 を除くn 乗根は全て原始n 乗根である.つまり,zp = 1 の解 1,ω,ω2,··,ωp¡1 ω = cos 2π p isin 2π p) から1 を除いたp − 1 個の数がそれにあたる.ω = cos π 4 isin π 4 は原始8 乗根のうちの & 反転の重要な性質 mathtrainjp この記事は,反転の初歩について非常によくまとめられているので,そちらをご覧ください.特に, 反転によって, 1−1:原点を通る直線は原点を通る直線にうつる 1−2:原点を通らない直線は原点を通る円にうつる 1−3
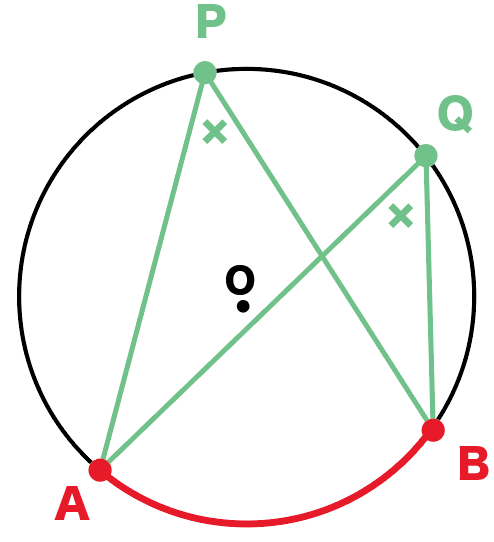
(ii)点qが円cの内部にあるとき ∠apb∠aqb であることが証明できました。 これを☆とおきます。 では、やっと円周角の定理の逆、 ならば、4点a、b、p、qは同じ円周上にある」 を証明します。 といってもあとは簡単です。「円に潜む性質!」 ひそ ~証明に用いる図形の性質を読み取る~ ☆本時のねらい:円周角の定理の証明において,用いられている図形の性質を読み取る ことができる。 ☆本時の工夫点:①図の中の角度を実測し円周角の定理を予想させることで,証明する垂心の性質《証明》 三角形の垂心がもつ性質の証明をします。 まずは「 四角形adhf,behd,cfheは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。
の外接円の周上の点 から,直線 , , に 垂線 , , を下ろす。 このとき,垂線の足, , , の 3 点が一直線上に存在 します。 このことをシムソンの定理といいます。証明は以下のようにすることができます。 線分 , をひく。 より, , , , は を直径とする円周上にある。Page 4 ここで,三角形abc の外接円は補助円の役目を果たしているが,角aの二等分線と辺bc の交点をd と するとき,'adc の外接円を補助円と考えて証明を試みてみよう. (e)補助円による証明 証明) 'adc の外接円と辺abとの交点をe とすると, 円周角の性質より, ed dc傍接円、傍心について 中学生へ 三角形の外角の二等分線の交点を「傍心ほ(ぼ)うしん」といい、傍心は全部で3つあり、下の図で ABCの傍心は点P、Q、R の3つです。 1990年ごろの中学の教科書にも傍心という用語は出てきませんが、傍接円と接線の長さ




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座



中学校数学 証明のコツ 入試問題 円
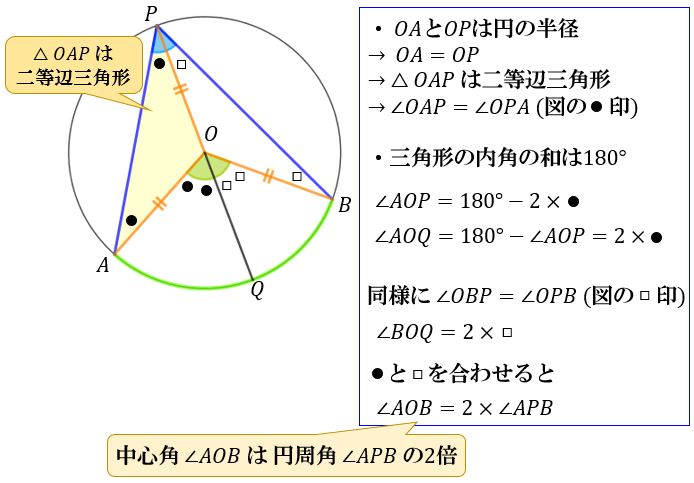
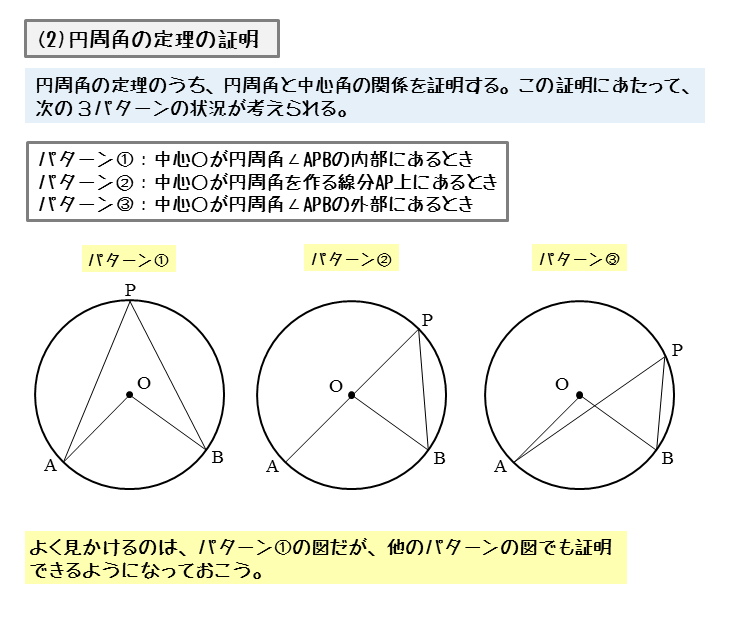
円周角の定理の証明の3パターン 「 円周角の定理 」を証明していくぞ。 3点A・B・Pがある円Oを想像してくれよな。 円周角と中心角の位置関係はつぎの3通りある。 点 PがOB上にあるとき 中心Oが∠APBの内側にあるとき 中心 Oが∠APBの外側にあるとき 円周角の定理1つ目の証明は以上になります。 円周角の定理の証明その2 次は、「同じ孤に対する円周角は等しい」という円周角の定理を証明していきます。 これは意外と簡単に証明できます。 まずは、 円の中心oと、点a、bを結んで補助線を引きましょう。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog
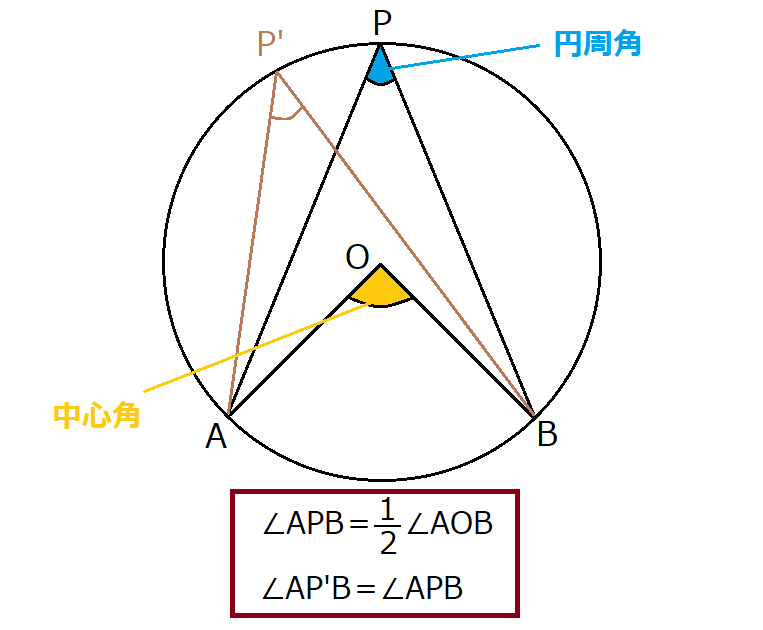
円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは,a c = 180 を説明 (証明)します。 円 周 角 : に 対直径pokを引くと,(ア)の証明と同様に 3+4で したがって ∠apb=1∠aob 2 <戻る> (ウ) 直径pokを引くと,(ア)の証明と同様に 6-5で したがって ∠apb=1∠aob 2 <戻る>



円周角の定理の証明を3つ紹介 逆も把握しよう ヒデオの情報管理部屋
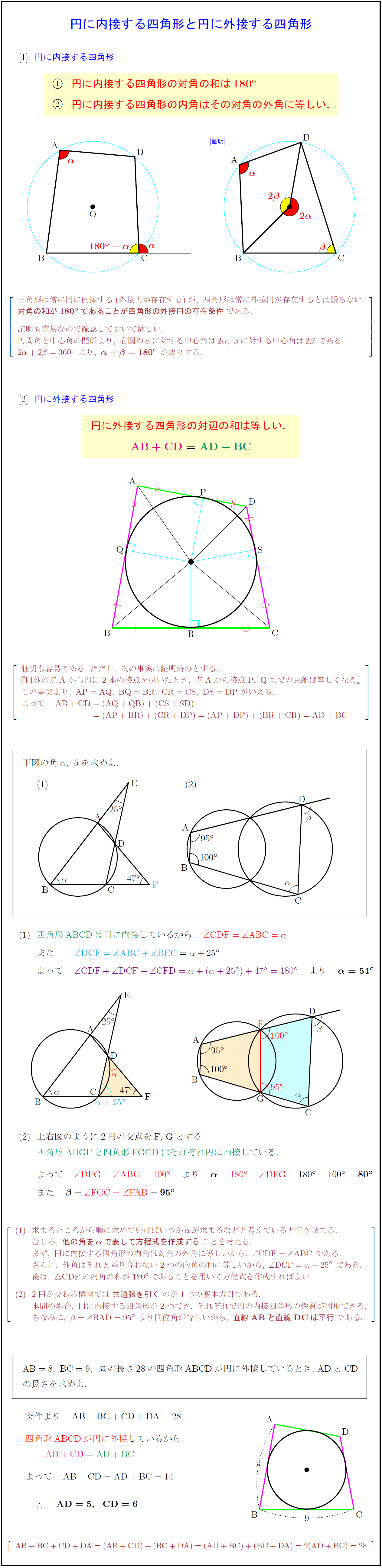



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月
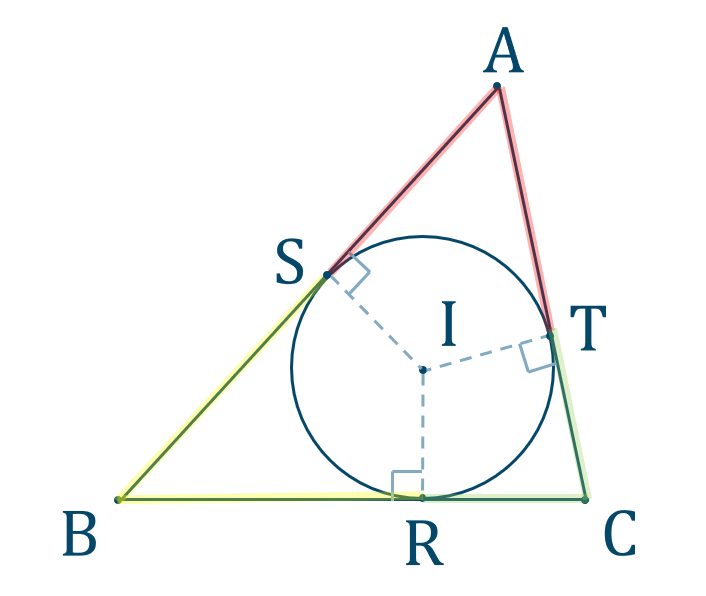
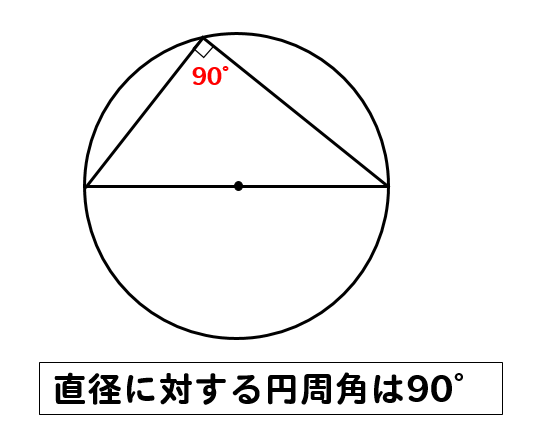
三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出逆に、「直角三角形の各頂点を通る円は、斜辺(直角に対する辺)がその円の直径になる」というのも重要な性質です。 円周角の定理の逆 図のように 「点a、点b、点p、点qにおいて、∠apq=∠aqbなら、すべての点は1つの円周上にある」 といえます。 ここからは少しマニアックな内容になりますが,アポロニウスの円の中心がどのような位置にあるか考えてみましょう.実は次の美しい事実が成り立ちます. アポロニウスの円の中心: m,n m, n を相異なる正の実数とする.平面上の 2 2 点 A,B A, B からの距離



円周角



円周角
内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離円の弦の性質 円の弦の垂直二等分線は円の対称の軸となり、円の中心を通る。 証明 円の円周上に点ABをとる。 弦ABの垂直二等分線 を引き、弦ABとの交点をPとすると、 OAPと OBPについて は垂直二等分線なので、 AP=BP ∠OPA=∠OPB=90°性質 (レベル1~2) 楕円の性質その1 楕円上の点から、2焦点までの距離の和は 一定であり、その値は長軸の長さ 2a 2 a に等しい。 長軸 とは、楕円内部にひいた2焦点を通る直線のことです。 (上の具体例を見た方が分かりやすい) 前半部分は楕円の定義より




中3数学 円の性質18 円の性質を利用した証明 すべて無料 星組の中学数学講座
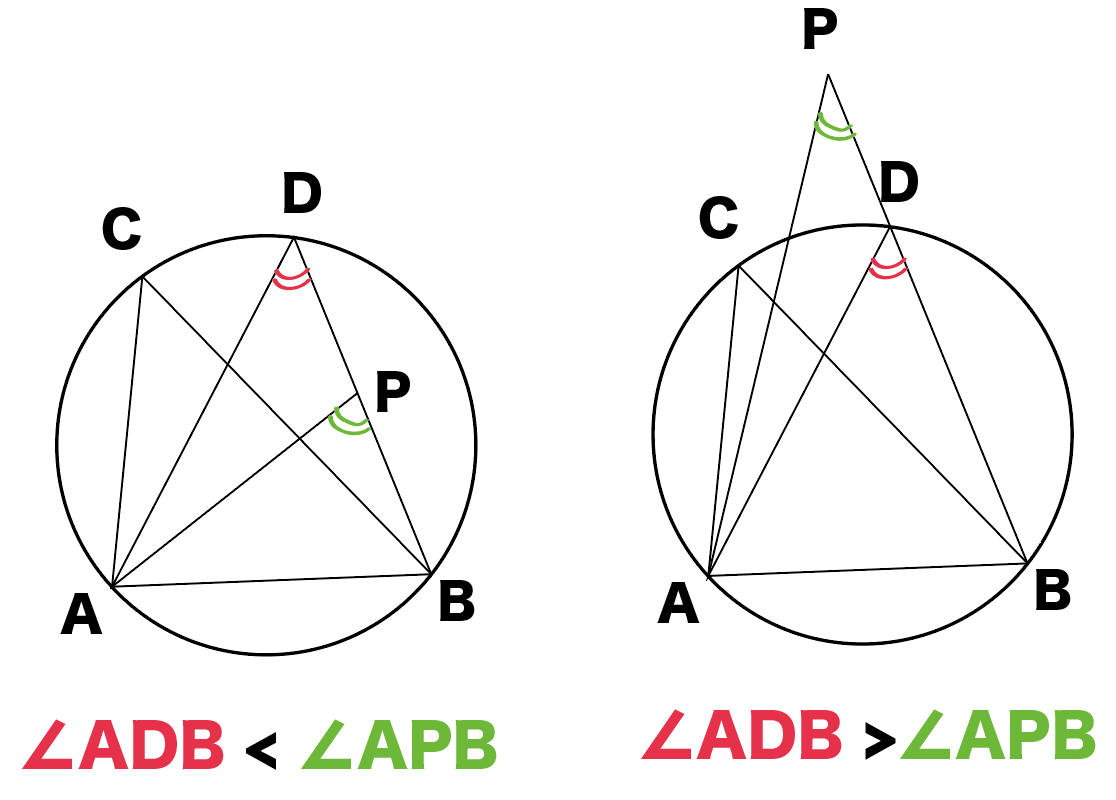



3分でわかる 円周角の定理の逆の証明 Qikeru 学びを楽しくわかりやすく
タレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者タレス ゆえに、 O O を中心とする A,B,C A, B, C を通る円が存在する。 垂直二等分線の交点 = 中心 (外心) 三角形の三辺の垂直二等分線の交点は、 外接円 の中心である。 この中心を 外心 という。 証明 ABC A B C の辺 AB A B の中点を M AB M A B とし、 辺 BC B C の中点を M




中3数学 円の性質と証明 練習編 映像授業のtry It トライイット




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




三角形の外接円の 4 つの性質 証明付 理数アラカルト



数学a 平面図形 円の性質 円の接線
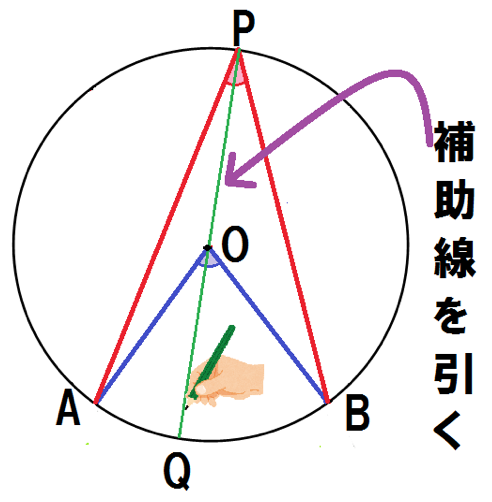



これでスッキリ 円周角の定理の証明の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




三角形の外心の性質と証明



円周角の定理の証明




高校数学復習記録 その9 桜花 現役バイト塾講師 Note




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学



中学校 第3学年 数学科指導プログラム 円周角



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理の証明




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく



1




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



円と三角形 角度 中学から数学だいすき




S A R Descubre Como Resolverlo En Qanda



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



3 24第1章式の計算の利用 図形の性質の証明 中学生




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット



数学指導案
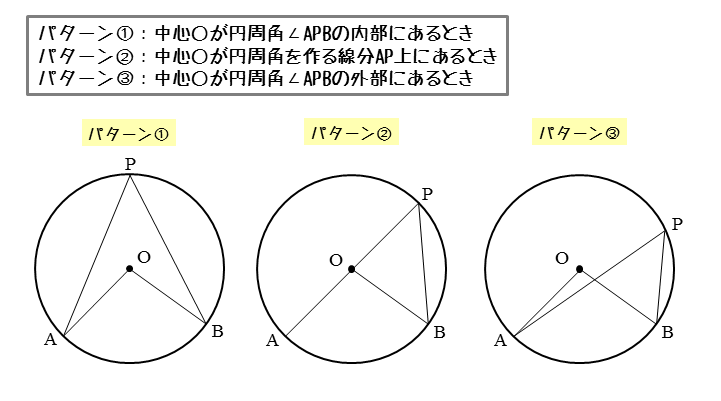



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube
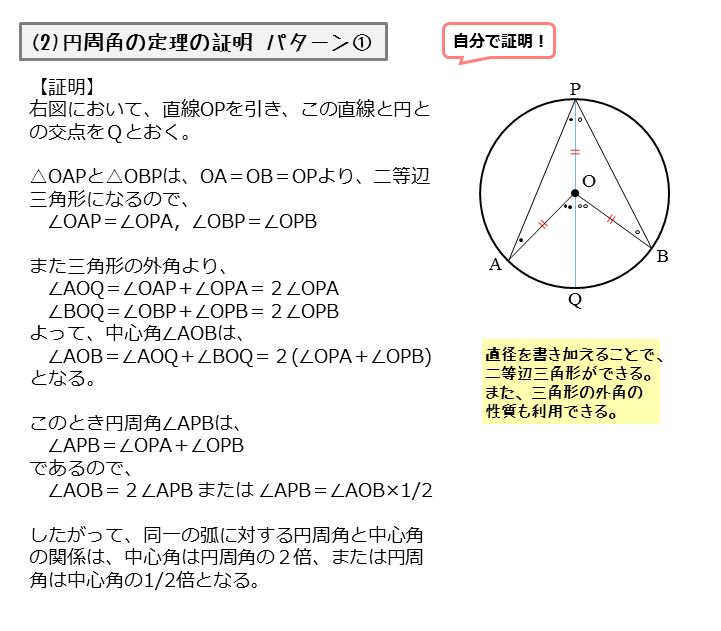



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



1
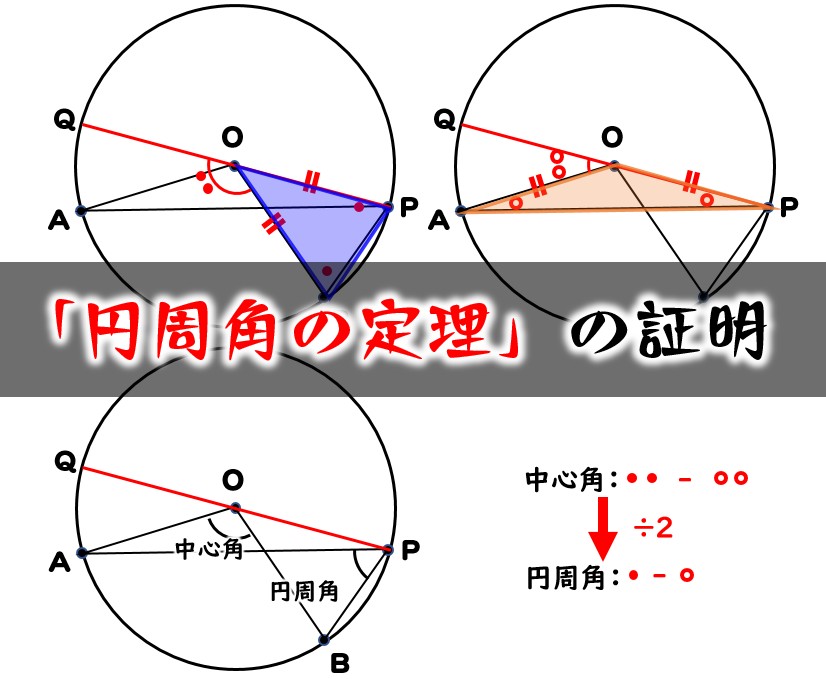



円周角の定理の証明 図で分かりやすく解説 数学fun



九点円の定理 思考力を鍛える数学



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



1



数学a円の性質の証明問題です 問題 弦abの垂直二等分線は Yahoo 知恵袋
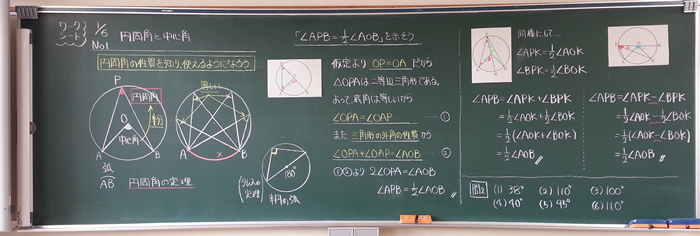



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館




中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット



方べきの定理の証明と例題 思考力を鍛える数学
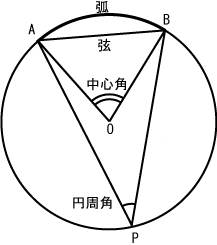



円 数学 Wikipedia




このような円の性質の証明の解くポイントはありますか Clear
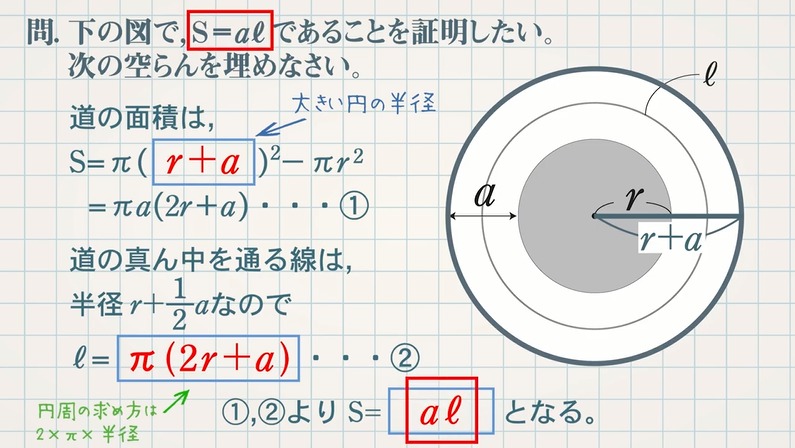



S Aℓの証明 式の計算の利用 図形編 教遊者




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
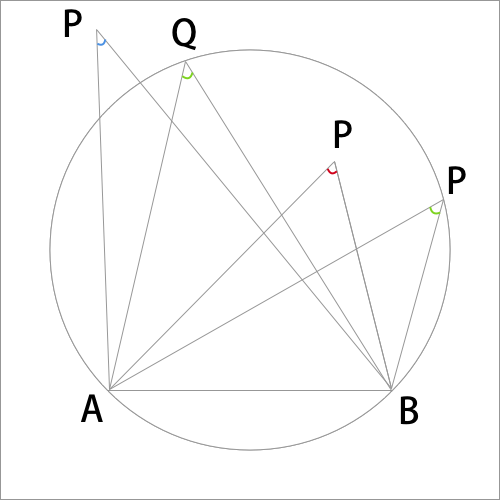



円周角の定理の逆の性質とその証明について




本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download
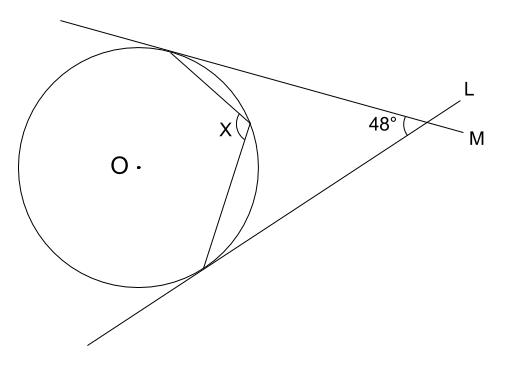



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円の性質の利用 チーム エン



1




数学 中3 56 円周角の定理 基本編 Youtube
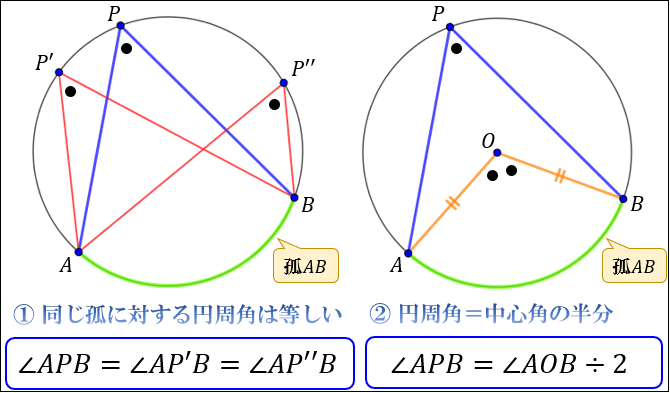



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




図形の性質がわかません 図の Oebが90度になる理由がわかりません Okwave




接線と円の関係 Jsciencer
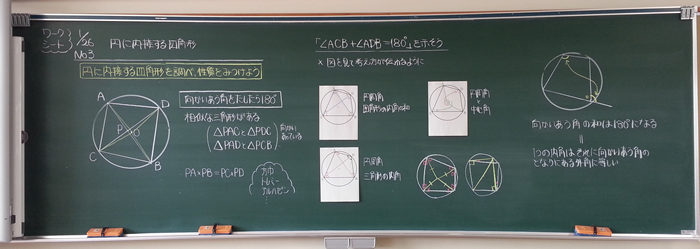



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館




高校数学a 共円条件 4点が同一円周上にある条件 受験の月
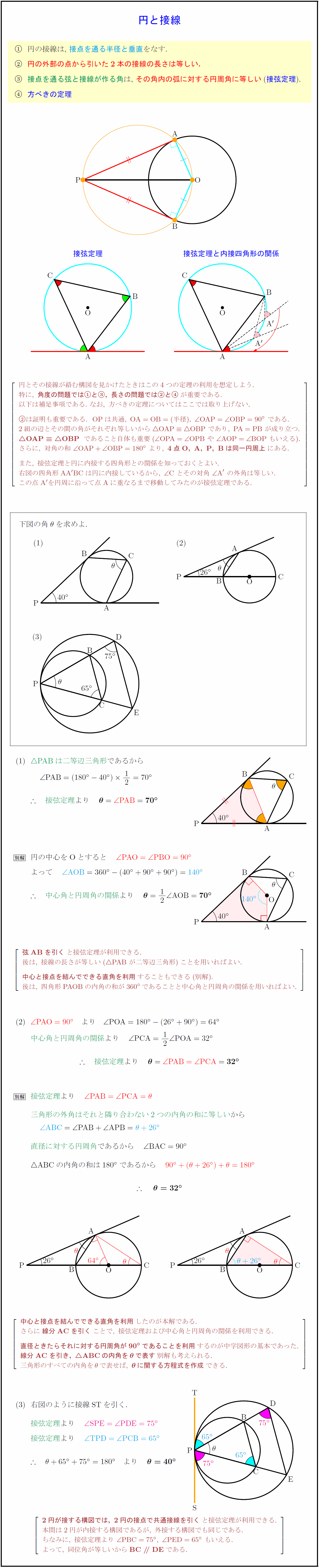



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
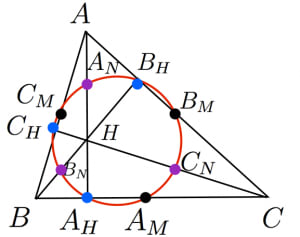



九点円の定理の証明と諸性質 高校数学の美しい物語
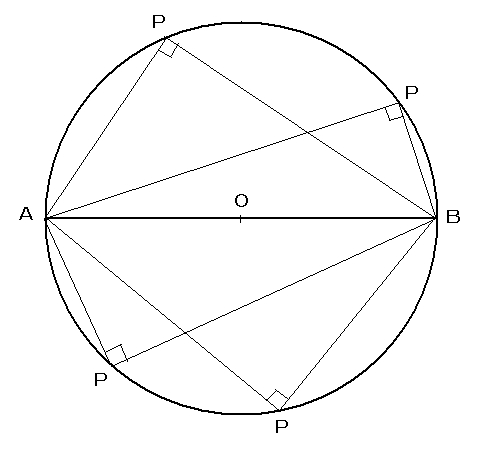



タレースの定理




公立入試問題の解説 円の性質 桃李塾のブログ
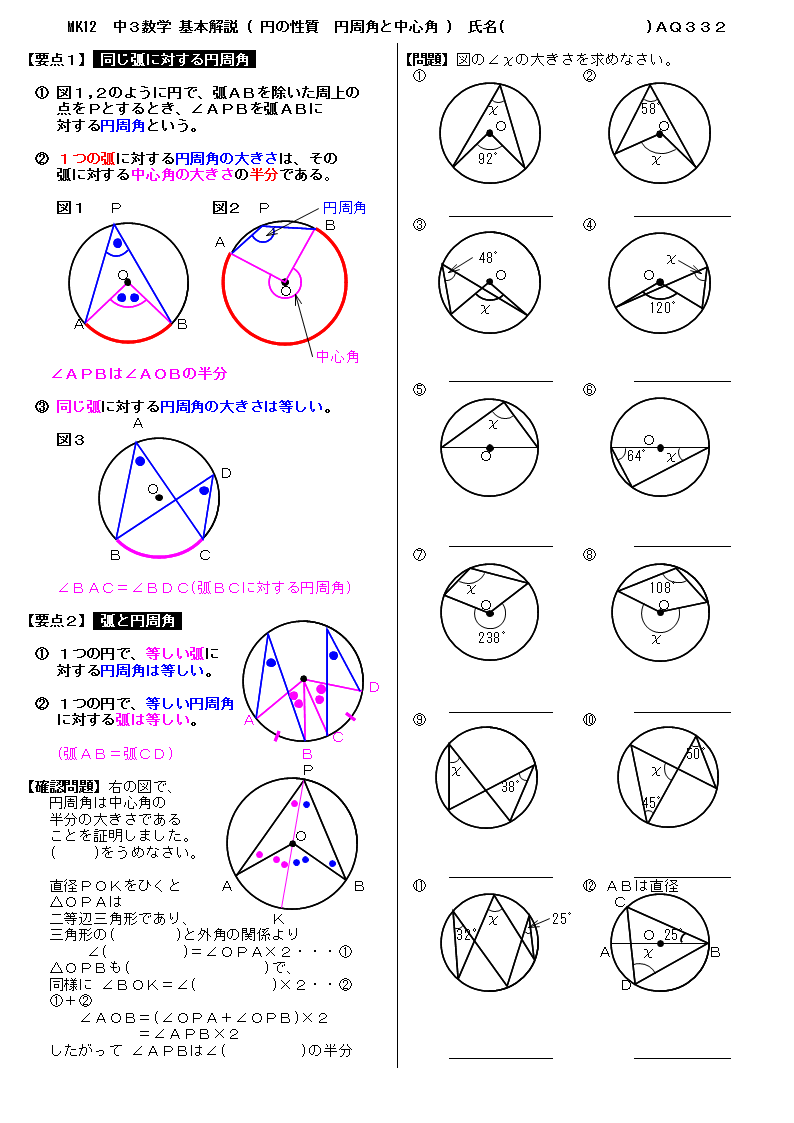



無料 中3数学 基本解説 問題プリント 332 円の性質 円周角と中心角




3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




これ説明してくれる人いますか なんでこうなるのか分かりません Clear




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中3 6章 円の性質




中3数学 円の性質16 円の性質を利用した証明 Youtube



円と相似 まなびの学園



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
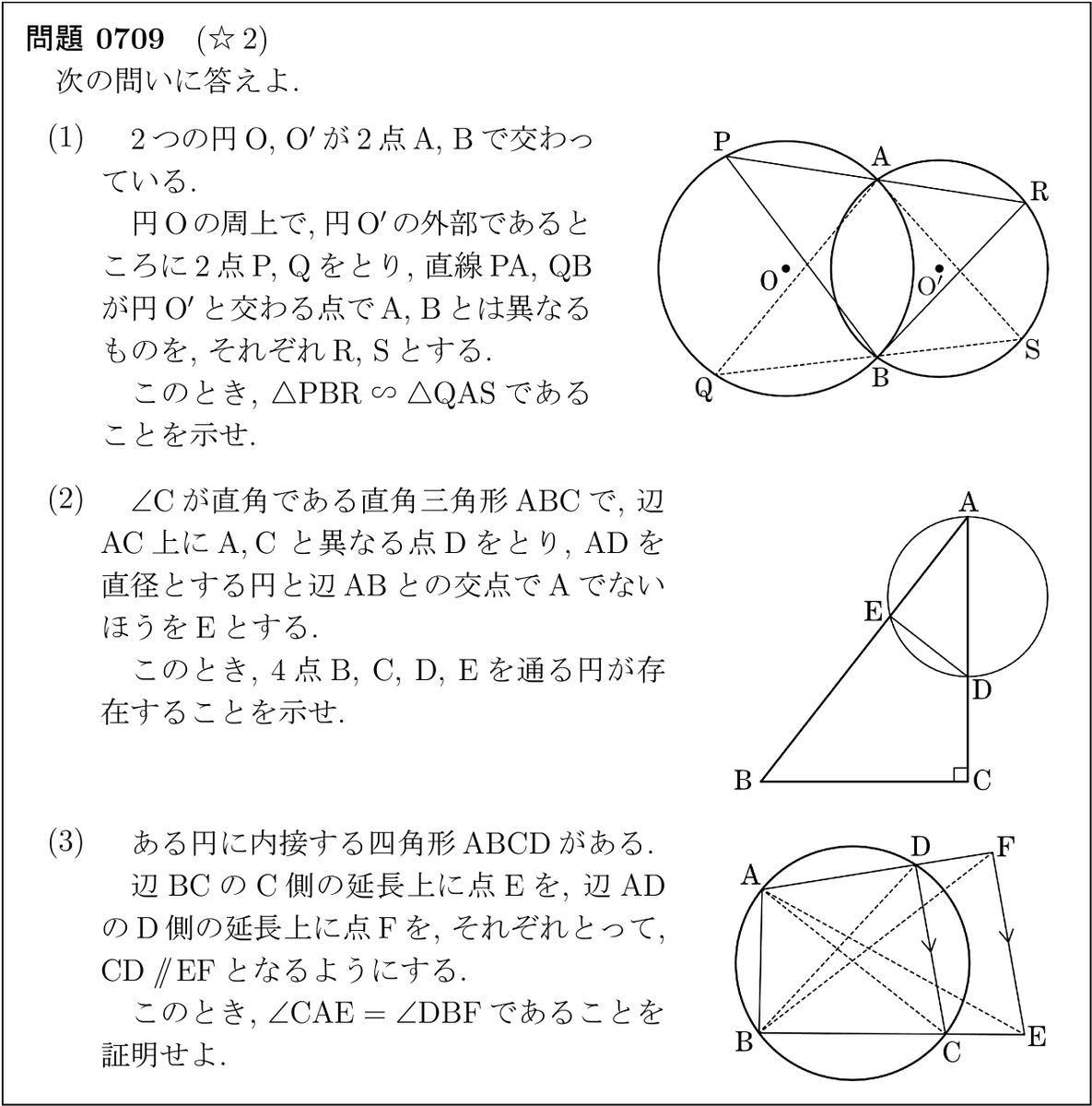



高校数学基本問題垂れ流し Ar Twitter 07 図形の性質 2 円 円周角 円に内接する四角形 4点が同一円周上にある条件と証明




平面図形23 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する
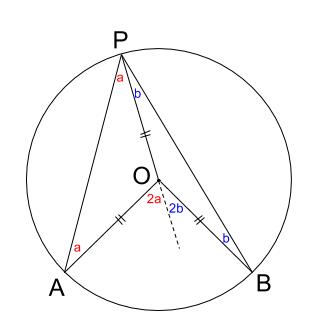



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su
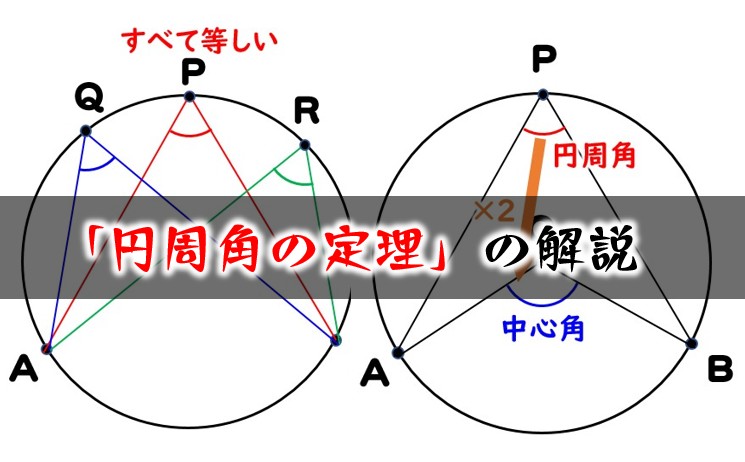



円周角の定理の解説 問題の解き方 数学fun




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




中3数学 円の性質8 円周角の定理の逆 4点が同じ円周上にあることの証明 すべて無料 星組の中学数学講座




円の性質 円周角 図形 数学 高校受験講座 東京先生




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
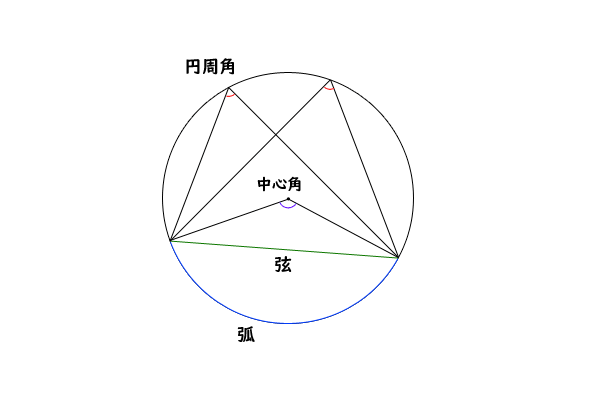



円周角の定理とその逆の証明 高校数学マスター




中学数学 よく出る円と相似の融合問題 Pikuu



外接円 外心について
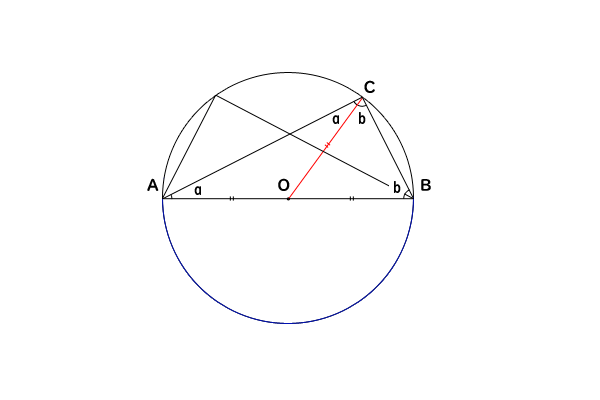



円周角の定理とその逆の証明 高校数学マスター




三角形の外接円の 4 つの性質 証明付 理数アラカルト




中学数学 円周角 中心角




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット




円の性質 数学の要点まとめ 練習問題一覧




世界一わかりやすい数学問題集中3 6章 円の性質
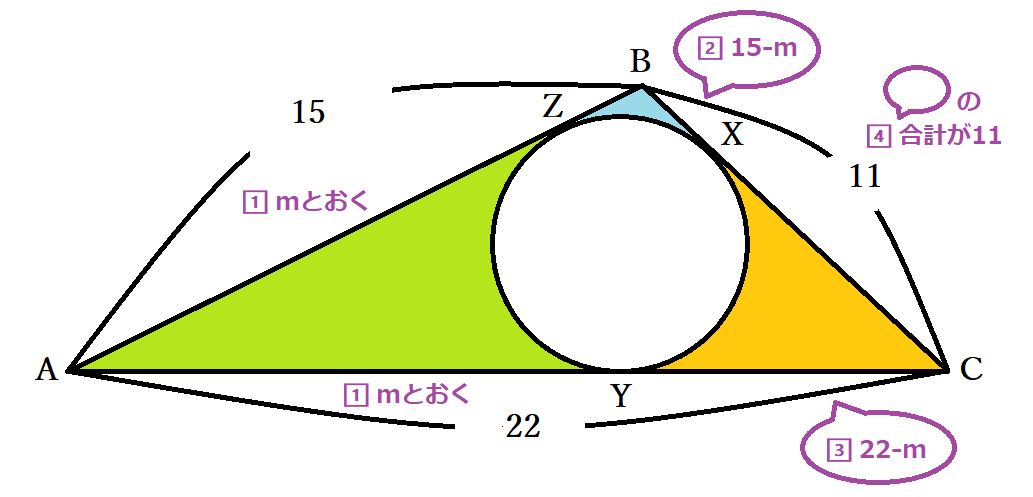



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog
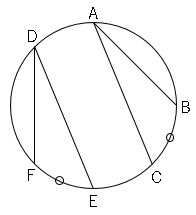



円の性質 数学の要点まとめ 練習問題一覧



内接円 内心



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス
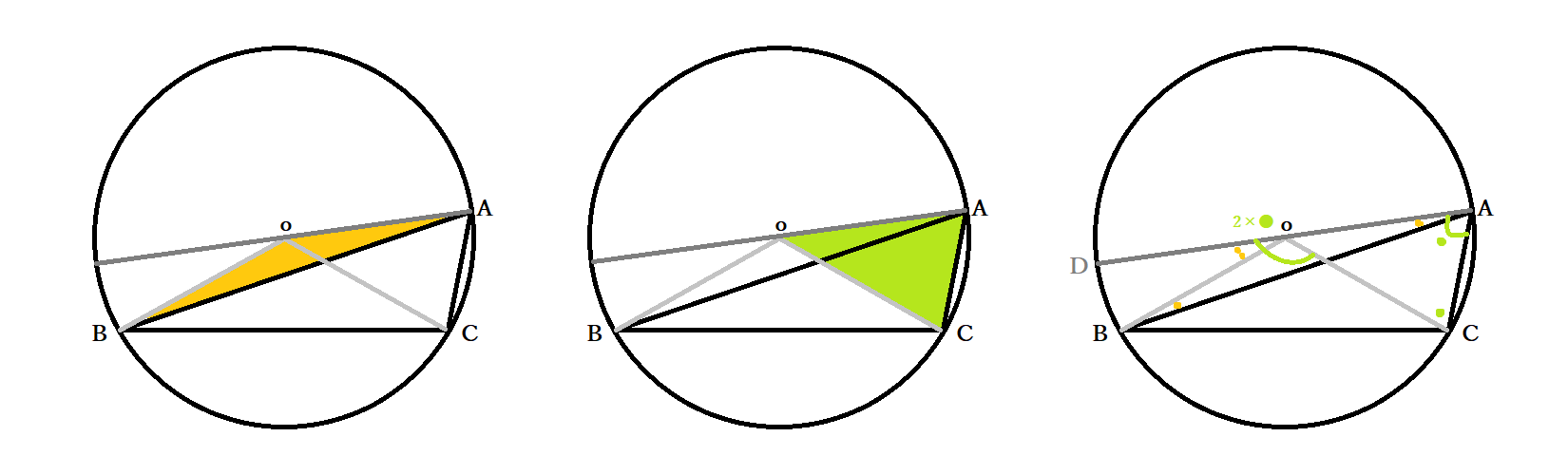



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



0 件のコメント:
コメントを投稿